Найти корни уравнения: a * x 3 + b * x 2 + c * x + d = 0
| Добавил: | DMT | ||||||||||||
| Дата создания: | 4 декабря 2007, 1:22 | ||||||||||||
| Дата обновления: | 1 марта 2008, 16:59 | ||||||||||||
| Просмотров: | 16072 последний сегодня, 0:44 | ||||||||||||
| Комментариев: | 0 | ||||||||||||
|
Найти корни уравнения: a * x 3 + b * x 2 + c * x + d = 0 с точностью до 0.01 . Вместо компонентов a , b , c и d записать заданные значения из таблицы 2.3. Корни найти методом половинного деления. Разработать блок-схему задачи, составить исходный код на языке ВС++, откомпилировать, получить *. exe -программу, получить решение. Выполнить проверку решения.
Найти корни уравнения: -0.5 x 3 – 3 x 2 +5 x + 1 = 0 с точностью до e = 0.01. Корни найти в два этапа: отделение корней и уточнения корней методом половинного деления. Разработать блок-схему задачи, составить исходный код на языке ВС++, откомпилировать, получить *. exe -программу, получить решение. Выполнить проверку решения. Этап 1 – метод отделения корней
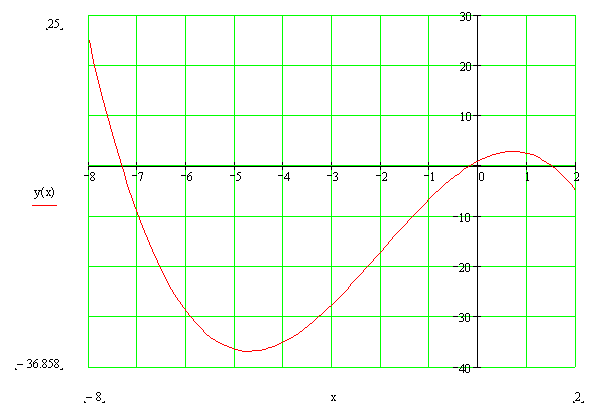
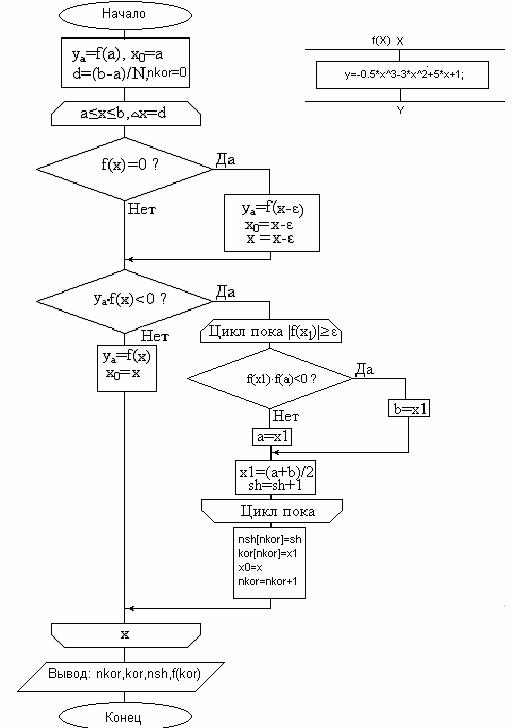
Если корень совпал с начальной точкой интервала a ( f ( a ) = 0), то он захватывается в интервал, который увеличивается на величину e . Следующий условный блок ( f ( a ) ? f ( b ) < 0) проверяет знаки на текущем интервале. Если знаки совпадают, то готовится к выборке следующий интервал, в противном случае в массив v заносятся координаты границ интервала, содержащего корень x . Массив v передается на второй этап – уточнение корней, который может выполняться различными методами – половинного деления, хорд, касательных и др. Этап 2 – метод уточнения корней В качестве метода уточнения корней предлагается использовать метод половинного деления. Сущность его следующая: интервал [ a , b ] , содержащий корень (рис. 2.3), делится пополам, и в полученной новой точке х 1 определяется значение функции f ( x 1 ). Если f ( a ) и f ( x 1 ) имеют одинаковые знаки, то интервал [ a , х 1 ] отбрасывается и х 1 становится новой точкой a , в противном случае отбрасывается интервал [ х 1 , b ] и х 1 становится новой точкой b . Новый интервал [ a , b ] делится пополам, и процесс повторяется до тех пор, пока | f ( x 1 ) |< e . Блок-схема алгоритма программы представлена на рис. 2.3. Программа должна иметь два вложенных цикла: внешний – с фиксированным числом циклов (цикл for ), по числу найденных корней программой отделения; внутренний – итерационный ( do while ) уточнения корней, число циклов подсчитывается счетчиком sh . Должны быть выданы: число корней, значения корней, число итераций при поиске каждого корня. Выполнить проверку путем подстановки значения корня в уравнение и определения погрешности. График полинома :
Блок схема :
Программа : #include <stdio.h>#include <math.h>double func(double g){ double y;y=-0.5*pow(g,3)-3*pow(g,2)+5*g+1; return y;} void main(void){ int sh,nkor,nsh[4],i;double d,ya,x0,x,x1,a,b,n,e,am,bm,kor[3];printf("\n\n\n_________________________________________________________\n"); nkor=0; a=-8; b=2; n=10; e=0.01; ya=func(a); x0=a; d=(b-a)/n; for (x=a;x<=b;x=x+d){if (func(x)==0){ya=func(x-e); x0=x-e; x=x-e; continue ;} if ((func(x0)*func(x))<0){am=x0; bm=x; sh=0; x1=(am+bm)/2; while (fabs(func(x1))>=e){if ((func(x1)*func(am))<0) bm=x1;else am=x1;x1=(am+bm)/2; sh=sh+1;} nsh[nkor]=sh; kor[nkor]=x1; x0=x; nkor=nkor+1;} else {ya=func(x); x0=x; continue ;}} printf("Vsego kornei\t%d\n",nkor); e=0; for (i=0;i<3;i++){ x=func(kor[i]); e+=x; printf("Koren' %d\tx=%1.8f\tsh=%d\\tProverka %1.5f \n\",i,kor[i],nsh[i],x); } printf("Srednyaa pogreshnost\' %1.8f \\n\",e/3); printf("_________________________________________________________\n"); scanf(\"%d\",sh); } | |||||||||||||

 Выход
Выход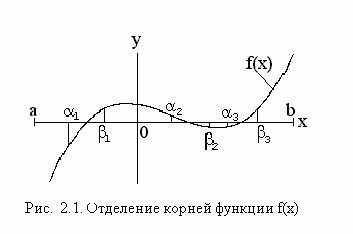 Функция
f ( x ) определена на интервале [ a , b ] (рис. 2.1). Разобьем его на N равных
частей, каждую из которых обозначим через [ a , b ] . Если функция f ( x )
принимает разные знаки на концах интервала, т.е. f ( a ) ? f ( b ) < 0, то
внутри этого интервала есть, по крайней мере, один корень уравнения f ( x ) = 0,
т.е. найдется хотя бы одно число ? , такое, что f ( ? ) = 0. Алгоритм поиска
интервалов [ a , b ] , на которых функция f ( x ) принимает разные знаки, т.е.
имеет один действительный корень, представлен на рис. 2.2. Все интервалы,
содержащие корни уравнения, записываются последовательно в массив v . В качестве
исходных данных для отделения корней примем функцию f ( x ), интервал поиска [ a
, b ], число разбиений интервала – N .
Функция
f ( x ) определена на интервале [ a , b ] (рис. 2.1). Разобьем его на N равных
частей, каждую из которых обозначим через [ a , b ] . Если функция f ( x )
принимает разные знаки на концах интервала, т.е. f ( a ) ? f ( b ) < 0, то
внутри этого интервала есть, по крайней мере, один корень уравнения f ( x ) = 0,
т.е. найдется хотя бы одно число ? , такое, что f ( ? ) = 0. Алгоритм поиска
интервалов [ a , b ] , на которых функция f ( x ) принимает разные знаки, т.е.
имеет один действительный корень, представлен на рис. 2.2. Все интервалы,
содержащие корни уравнения, записываются последовательно в массив v . В качестве
исходных данных для отделения корней примем функцию f ( x ), интервал поиска [ a
, b ], число разбиений интервала – N .