ТЕОРИИ ПЕРВОГО ПОРЯДКА |
|
Модели теории первого порядка определяются как множества с
заданными на них операциями и отношениями, удовлетворяющими аксиомам. К
таким моделям относятся, например, частично упорядоченные множества и
булевы алгебры.
Теории первого порядка возникли с целью формализации и
строгого обоснования математики. В 1901 году Дедекинд предложил первое
обоснование арифметики, известное теперь под названием системы аксиом
Пеано. В 1908 году Цермело сформулировал аксиомы теории множеств. Так было
установлено, что множество натуральных чисел и класс всех множеств тоже
являются моделями теорий первого порядка. Это стимулировало развитие
теории моделей, основные теоремы которой были доказаны Лёвенгеймом (1915
г.), Скулемом (1920 г.), Гёделем (1930 г.), Мальцевым (1936
г.).
Главное внимание в данной главе будет уделено доказательствам
теоремы Мальцева о компактности, теорем Гёделя о непротиворечивости
исчисления предикатов и о полноте теории первого порядка. Отметим теоремы
Лёвенгейма-Скулема, из которых следует существование счётной модели теории
множеств и несчётной модели теории натуральных чисел. Рассмотрим метод
резолюций Робинсона (1965 г.) автоматического доказательства предложений
исчисления предикатов.
Теги:Термы. Предикаты. Унификация. Исчисление
высказываний. Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
|
1. Термы и предикаты
Термы и их унификация
Упрощённо можно сказать, что термы – это
алгебраические выражения, определяющие функции, значения которых
вычисляются с помощью операций. Например, в булевой алгебре А определены
операции: З : A2 ® A, И :
A2 ® A, Ш : A ® A, и из этих
операций можно составлять термы, например, Шx2,
(x1 З x2), (x1 З
x2) И (Шx4 З
x0). Перейдём к точным определениям.
Пусть X =
{x0, x1, ...} – счётное множество, элементы которого
будут называться переменными, F – произвольное множество, элементы
которого будут называться функциональными символами, # : F
® w – произвольная функция. Элементы f О F, для
которых # f = n > 0, называются n-арными операциями. Например, для
булевой алгебры множество функциональных символов будет равно: F =
{З, И, Ш}, значения функции # равны
#(З) = 2, #(И) = 2, #(Ш) = 1, поэтому все
элементы из F – операции. Символы c О F, для которых #(с) = 0,
называются символами констант. Термы определим по индукции: |
1) переменные xi и символы констант являются термами;
2)
если ti, t2, ... , tn – термы и f –
n-арная операция, то f(ti, t2, ... , tn)
– терм;
3) кроме построенных с помощью правил 1 – 2, других термов
нет.
В определении терма участвует префиксная форма операции. Заметим,
что бинарные операции записываются обычно в инфиксной форме. Например,
вместо И (x0, З(x1,
x2)) применяется запись: x0 И
(x1 З x2). Учитывая приоритеты операций,
скобки часто опускают, в частности, приведённая запись равносильна
выражению: x0 И x1 З
x2, ибо приоритет операции З выше приоритета
И .
Согласно определению терма, множество всех термов T(F)
содержит множество переменных X. Подстановкой называется отображение v: X
® T(F) такое, что для всех x О X, за исключением
элементов некоторого конечного подмножества из X, имеет место v(x) = x.
Распространим подстановку v до некоторой функции v': T(F) ® T(F),
полагая |
1). если t О X, то v'(t) = v(t);
2). если t – символ
константы, то v'(t) = t;
3). если t = f(t1, ... ,
tn) для некоторой n-арной операции f и термов t1,
... , tn О T(F), то v'(t) = f(v'(t1), ... ,
v'(tn))
Терм v'(t) называется результатом применения
подстановки v к терму t. Например, результатом
подстановки
v(x0) = x0, v(x1) =
x1 И x2, v(x2) = x0
З x1
в терм x0 З
Шx2 будет терм: v'(x0 З
Шx2) = v'(x0) З
Шv'(x2) = x0 З
Ш(x0 З x1). Если значения
v(xi) не указаны, то по умолчанию v(xi) =
xi. Подстановку записывают как множество пар xi =
ti, например: v = {x1 = x1 И
x2, x2 = x0 З
x1}.
Пусть заданы два терма s и t, и пусть надо найти
подстановку, делающую эти термы равными. Эта задача решается следующим
образом.
Подстановка v называется унификатором термов s и t, если v'(s)
= v'(t). Унификатор v называется наибольшим общим унификатором термов s и
t и обозначается: m.g.u.(s, t) = v, если для любого другого унификатора w
термов s и t существует такая подстановка a, что a'
° v' = w'. Если для термов s и t существует хотя бы один
унификатор, то среди унификаторов существует наибольший общий. Для его
нахождения предлагается следующий алгоритм.
Алгоритм унификации термов
с использованием стека
Вход: термы s, t.
Выход: подстановка
h, записанная как список пар xi = ti, если
t и s обладают наибольшим общим унификатором. Процедура возвращает отказ,
если унификаторов нет.
Действия: h = Ж; запомнить
пару (s = t) в стек;
Пока стек не пуст, выполнять цикл:
Тело цикла:
Извлечь из стека пару термов (s = t) и произвести одно
из следующих действий, в зависимости от выполнения одного из условий
I.
если s – переменная, t – терм, не содержащий вхождений
s , то все вхождения переменной s в стеке заменяются на
t и все вхождения s в h заменяются на
t, затем подстановка s = t добавляется к списку
подстановок в h;
II. если t – переменная, а
s – терм, то произвести действия, как в I, поменяв ролями
s и t (к h добавляется пара t =
s);
III. если s и t – составные термы,
s = f(s1, s2, ..., sn) и
t = f(t1, t2, ..., tn), то все
пары si = ti, 1 Ј i Ј n,
запоминаются в стек;
VI. если s и t – одинаковые
символы констант или переменных, то ничего не делать;
V. во всех
остальных случаях производится выход из цикла и возвращается
отказ.
Конец тела цикла.
Если выход из цикла произошёл не после
выполнения условия V, то h содержит элементы xi =
ti искомой подстановки.
Пример
s = (a З b)
И ((a З b) З d), t = (a З b)
И (c З (a З b)). |
- Устанавливаем h = Ж; запоминаем в стек пару (s =
t);
- извлекаем (s = t) из стека, имеет место случай III, запоминаем в
стек пары a З b = a З b и ((a З b) З
d = c З (a З b));
- извлекаем из стека ((a З b) З d = c З (a
З b)), имеет место случай III, запоминаем в стек (a З
b = c) и (d = a З b);
- извлекаем из стека (d = a З b), имеет место случай I,
h = {(d = a З b)};
- извлекаем из стека (a З b = c), имеет место случай II,
h = {(d = a З b), (c = a З b)};
- извлекаем из стека (a З b = a З b), изменений в
h нет;
- стек пуст, возвращаем h = {(d = a З b), (c = a
З b)}
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
Система уравнений
Пусть задано несколько пар термов (s1,
t1), (s2, t2), ..., (sn,
tn) и необходимо найти подстановку w, которая превращает все
пары термов (si, ti) в равные w'(si) =
w'(ti). Эта задача называется системой уравнений: s1
= t1, s2 = t2, ..., sn =
tn.
Унификатором системы уравнений называется подстановка v,
которая является унификатором пар (si, ti) для всех
1 Ј i Ј n. Система уравнений (si,
ti), 1 Ј i Ј n, называется находящейся в
разрешённой форме, если каждое из этих уравнений имеет вид: ui
= ti для некоторого элемента ui О X, причём
переменная ui не входит в терм ti ни при каком i.
Такая система имеет унификатором подстановку: {u1 =
t1, ..., un = tn}, которая будет наиболее
общим унификатором этой системы. Редукцией термов называется замена
уравнения f(s1, ..., sn) = f(t1, ...,
tn) системой уравнений: s1 = t1,
s2 = t2, ..., sn =
tn.
Недетерминированный алгоритм решения множества
уравнений
Вход: множество уравнений s1 = t1, ...,
sn = tn.
Выход: множество уравнений в разрешённой
форме h = {u1 = t1, ...,
um = tm}.
Действия: пока истинно условие
применимости хотя бы одного из перечисленных далее преобразований,
выполнять в цикле альтернативы.
Начало цикла: |
I. если существует уравнение вида: t = x, где t – не переменная, а x –
переменная, то заменить это уравнение на x = t; в противном случае
II.
если существует уравнение вида: x = x, где x – переменная, то удалить это
уравнение из системы уравнений; в противном случае
III. если существует
уравнение вида: s = t, в котором s и t не являются переменными, то если
корневые функции термов s и t различны, тогда возвращается “отказ”, в
противном случае осуществить преобразование редукции термов;
VI. если
существует уравнение вида: x = t, такое, что переменная x не входит в
другие уравнения системы и терм t отличен от x, то если переменная x
входит в t, тогда возвращается “отказ”, в противном случае осуществить
преобразование элиминации переменной.
Конец цикла. (Возвращается
“успех”, преобразованная система уравнений будет искомым
унификатором.)
Здесь под элиминацией переменной понимается переход от
системы уравнений к системе, полученной после подстановки x =
t.
Пример
Рассмотрим систему, состоящую из одного
уравнения:
((a З b) И d) И (a З b)
= (c И (a З b) И (a З b)}
1)
Применяем случай III, делаем редукцию, получаем: h = {(a
З b) И d) = c И (a З b), a З
b = a З b}.
2) Применяем случай III, получаем: h = {a
З b = с, d = a З b, a З b = a З
b}.
3) Применяем случай III для последнего уравнения и повторяем 2 раза
случай II, это приводит к h = {a З b = с, d = a
З b}.
4) Применяем случай I, получаем ответ: h = {c =
a З b, d = a З b}.
Теги:Термы. Предикаты. Унификация. Исчисление высказываний. Семантика.
Семантика языка. Теория групп. Робинсон. Метод резолюций.
Предикаты и отношения
Функция n переменных, принимающая значения 0 и
1, называется n-местным предикатом. Каждому отношению R Н
An соответствует предикат, равный характеристической функции
подмножества R. Ясно, что определение n-местного предиката
P(x1, ..., xn) на множестве А равносильно заданию
отношения:
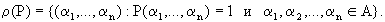
Пусть P(x1, ..., xn) и
Q(x1, ..., xn) – предикаты. Конъюнкцией P и Q
называется предикат (P&Q)(x1, ..., xn)
P(x1, ..., xn) & Q(x1, ...,
xn), дизъюнкцией – предикат (P Ъ Q)(x1,
..., xn) = P(x1, ..., xn) Ъ
Q(x1, ..., xn), отрицание определяется с помощью
предиката (ШP)(x1, ..., xn) =
{(x1, ..., xn) : P(x1, ...,
xn) = 0}.
Для предикатов определяются кванторы существования
и всеобщности. Пусть P(x1, ..., xn) – n-местный
предикат. Запись: $x1P(x1, ...,
xn) означает, что существует x1, для которого
P(x1, ..., xn) = 1, запись:
"x1P(x1, ..., xn) означает, что
P(x1, ..., xn) = 1 для всех x1.
Аналогично определяются предикаты $xiP(x1,
..., xn) и "xiP(x1, ...,
xn), при 1 Ј i Ј n. В этих случая говорят,
что переменная xi связана квантором. Предикаты
$xiP(x1, ..., xn) и
"xiP(x1, ..., xn) будут зависеть
от n-1 переменных. В случае, когда x П {x1, ...,
xn}, положим $x P(x1, ..., xn) =
P(x1, ..., xn) и "x P(x1, ...,
xn) = P(x1, ..., xn). Тем самым мы
определим предикаты $x P(x1, ..., xn) и
"x P(x1, ..., xn) для любых символов
переменных x. Отношение, соответствующее предикату
$x1P(x1, ..., xn) будет
проекцией отношения, определяемого P, на область (x2, ...,
xn), оно будет равно объединению по всем a О
A отношений, определяемых предикатами P( a, x2, ...,
xn). Предикату "x1P(x1, ...,
xn) соответствует отношение, равное пересечению этих отношений.
Таким образом,
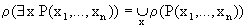 ; ;
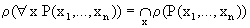 . .
|
|
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
2. Язык логики предикатов
Определим синтаксис языка первого порядка. Алфавит языка первого
порядка состоит из логических символов Ъ , Ш ,
$ , = , из символов переменных B1 Ъ
B2 Ъ ... Ъ Bk и из нелогических
символов. К логическим символам отнесём символы скобок и запятой. В
качестве символов переменных будем использовать также x, y, z, u, v и т.д.
Логические символы одинаковы для всех языков первого порядка.
Нелогическими называются символы операций, символы предикатов и символы
констант. Язык первого порядка L задаётся как множество нелогических
символов. Если L = Ж , то L называется языком чистого
равенства.
Каждому s О L ставится в соответствие #(s)
О w . Если s – константа, то #(s) = 0. Если R – символ
предиката, такого, что #(R) = n, то R называется символом n-местного
предиката. Если f – символ операции, и #(f) = n, то f называется символом
n-арной операции. Для предикатов и операций число #(R) (соответственно
#(f)) больше 0, и оно называется местностью (соответственно арностью).
Объединение множеств символов операций и констант составляет множество
функциональных символов, позволяющее строить термы языка L на множестве
{x0, x1, ..., xn, ...}.
К предикатам
языка L мы всегда относим бинарный предикат x0 = x1
(равенство). Определим формулы языка L.
Атомной формулой языка L
называется выражение вида: R(t1, t2, ...,
tn), где t1, t2, ..., tn –
термы языка L, а R О L – символ n-местного предиката. В
частности, выражение t1 = t2 будет атомарной
формулой для любых термов языка L. Множество всех формул языка L
определяется как наименьшее множество выражений, которое содержит все
атомные формулы и удовлетворяет условиям: если q и y –
формулы, а x – переменная, то выражения (q Ъ
y), Шq , $xq – формулы. Формулы
q и y называются подформулами формулы (q
Ъ y), формула q – подформулой формул
Шq и $x q .
Будем предполагать, что другие
логические связки служат сокращениям:
( q & y)
для Ш(Шq Ъ Шy),
( q
® y ) для (Шq Ъ
y),
" x q для Ш$x Шq
.
Формула Шx = y обычно записывается как x № y.
Примеры формул:
" x $ y P(x, y, x И z),
$ x (y Ј x ® y = x).
Замена
переменных
Переменная, содержащаяся в формуле, называется свободной,
если она не связана квантором, в противном случае она называется
связанной. Переменная может входить в формулу несколько раз, в этом случае
аналогичные определения применяются к каждому вхождению. Например, в
формуле
y (y = z) ® $ z (z < x)
первое
вхождение переменной z свободно, а второе – связанное. Переменная x
является свободной, а y – связанной. Формальное определение свободных и
связанных переменных следующее: |
1) все вхождения переменных в атомных формулах свободны;
2)
свободные вхождения x в Шq есть в точности свободные вхождения x
в q;
3) свободные вхождения x в (q Ъ
y) состоят из свободных вхождений x в q и свободных
вхождений x в y;
4) если x и y – различные переменные, то
свободные вхождения x в формулу $ y q соответствуют
свободным вхождениям x в формулу q;
5) в формуле $ x
q нет свободных вхождений переменной x.
Запись: q(x)
указывает на то, что формула q содержит свободные вхождения
переменной x. Если c – символ константы, то q(с) означает
формулу, полученную заменой всех свободных вхождений x в q на с.
Например, если q(x) = $ y((y = x) & " x (x
= y)), то q(c) = $ y((y = c) & " x (x =
y).
Мы пишем: q(x1, ..., xn) для
указания того, что q содержит свободные переменные среди
x1, x2, ..., xn. Применяется запись:
q(x1/t1, ..., xn/tn)
для обозначения формулы, в которой все свободные вхождения каждой из
переменных xi формулы q заменяются на терм
ti, 1 Ј i Ј n. Таким образом, q(с)
является сокращением обозначения q(х/с).
Формула, не
содержащая свободных переменных, называется предложением.
Может
случиться, что при замене переменной термом нарушается очевидный принцип,
согласно которому замена переменной в равных формулах даёт равные формулы.
Например, пусть t = f(y), q(z) = $ y(y < z). Тогда
после замены получаем: q(f(y)) = $ y(y < f(y)). С
другой стороны, q(z) = $ x(x < z), и, значит,
q(f(y)) = $ x(x < f(y)). Получаем не равные формулы.
Поэтому перед подстановкой терма t(y1, ..., yn) в
формулу q(х) связанные переменные, содержащиеся в {y1,
..., yn} будем переименовывать на символы, не встречающиеся в
{y1, ..., yn}.
Другой выход следующий: терм t
называется свободным для переменной x в формуле q(х), если
никакое свободное вхождение x в q не лежит в области действия
кванторов "xi и $xi, где
xi входит в t. В этом случае замена q(х/t)
допускается.
При подстановках констант противоречия не
возникают.
Замечание. Применяемые в анализе и алгебре обозначения: (
"x О A) q и ($x О
A)q служат сокращениями соответственно формул "x((x
О A) ® q) и $x((x О A)
& q). Например, 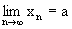 будет определяться формулой:
будет определяться формулой: 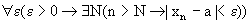 . .
Исчисление предикатов
Для того чтобы определить
формальную теорию, связанную с языком первого порядка, введём логические
аксиомы и правила вывода языка L. Логические аксиомы подразделяются на 3
группы:
1). Аксиомы предложений: всякая формула q языка L,
которая может быт получена из некоторой тавтологии исчисления высказываний
K (описанного в разд. 3 с помощью аксиом К1 – К10) в результате
подстановки формул языка L на место высказывательных символов, есть
логическая аксиома языка L. Всякая такая формула называется тавтологией
языка первого порядка L.
2). Аксиомы кванторов |
- если q и y – формулы языка L, то имеют место
следующие аксиомы:
(" x ( q ® y))
® (q ® " x y), если х не
входит свободно в q;
(" x ( q ®
y )) ® (($ x q) ®
y), если х не входит свободно в y;
- для каждой формулы q(х) и терма t, свободного для x, имеют
место кванторные аксиомы:
" х q(х) ®
q(t);
q(t) ® $ х q(х).
3). Аксиомы равенства |
t = t для любого терма t;
(t = s) & q(t) ®
q(s), для любых формул q(х) и термов s, t, для которых х
свободна в q, а s и t свободны для х (здесь q(t)
означает формулу q(x/t)).
Правила вывода
(MP) Из формул q и q ®
y выводится y (Modus Ponens).
(Gen) Из формулы
q выводится " x q (правило обобщения).
Таким
образом, определена формальная теория, (разд.3.4), в которой есть формулы,
аксиомы и правила вывода. Эта теория называется исчислением предикатов
L.
Запись: е 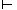 q
означает, что существует вывод формулы q из логических аксиом и
формул из множества е. Если Ж q
означает, что существует вывод формулы q из логических аксиом и
формул из множества е. Если Ж 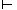 q,
то q – теорема исчисления предикатов L. Множество е
называется противоречивым, если для каждой формулы q языка L
существует вывод: е q,
то q – теорема исчисления предикатов L. Множество е
называется противоречивым, если для каждой формулы q языка L
существует вывод: е 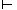 q.
В противном случае е называется непротиворечивым. Предложение
q называется непротиворечивым, если множество {q}
непротиворечиво. Множество формул е называется максимально
непротиворечивым, если оно не является собственным подмножеством
некоторого непротиворечивого множества. q.
В противном случае е называется непротиворечивым. Предложение
q называется непротиворечивым, если множество {q}
непротиворечиво. Множество формул е называется максимально
непротиворечивым, если оно не является собственным подмножеством
некоторого непротиворечивого множества.
Легко доказать следующие
свойства непротиворечивых множеств:
1) Множество е
непротиворечиво, если и только если каждое его конечное подмножество
непротиворечиво.
2) Пусть q – предложение. Тогда множество
е И {q} противоречиво, если и только если
е 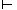 Шq . Шq .
3) Пусть е – максимально
непротиворечивое множество. Тогда для любых предложений q и
y имеет место:
(i) е 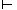 q,
если и только если q О е; q,
если и только если q О е;
(ii) q
П е , если и только если Шq О
е;
(iii) (q & y) О е ,
если и только если q О е и y
О е ;
4) Каждое непротиворечивое множество
предложений содержится в некотором максимальном непротиворечивом множестве
предложений.
Теорема (о непротиворечивости исчисления предикатов).
Нет формул q исчисления предикатов L, для которых существуют
выводы: 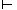 q и
q и 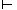 Шq. Шq.
Доказательство. Каждой формуле q
поставим в соответствие формулу h( q) исчисления высказываний K,
множество символов P которого состоит из предикатов R О L.
Формулу h( q) определим по индукции:
1) h(R(t1,
..., tn)) = R для атомных формул;
2) h(
q1 Ъ q2) = h(
q1) Ъ h( q2), h(
Шq) = Шh( q),
h( q1
® q2) = h( q1) ®
h( q2),
h( q1 &
q2) = h( q1) &
h(q2), для любых формул q1,
q2, q;
3) h( "xq) = h(
q), h($x q) = h(q).
Для всякой
логической аксиомы q формула h(q) будет тавтологией в K.
Если бы для некоторой формулы q существовали выводы 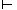 q и q и 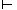 Шq,
то формулы h(q) и Шh(q) были бы тавтологиями в
исчислении высказываний. Поскольку исчисление высказываний
непротиворечиво, это невозможно. Стало быть, нет формул q, для
которых существуют выводы: Шq,
то формулы h(q) и Шh(q) были бы тавтологиями в
исчислении высказываний. Поскольку исчисление высказываний
непротиворечиво, это невозможно. Стало быть, нет формул q, для
которых существуют выводы: 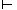 q и q и 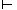 Шq
. Шq
.
|
|
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
3. Семантика языка логики предикатов
Моделью А языка L первого порядка называется пара, состоящая из
множества А, называемого универсумом, и функции (-)A,
сопоставляющей |
- каждому символу константы c О L некоторый элемент
cA О A;
- каждому символу n-арной операции f из L функцию fA :
An ® A;
- каждому предикатному символу R из L отношение RA
Н An.
Символ “=” интерпретируется как логический символ, такой, что
(=)A = {(x, x): x О A}.
Пример 1
Пусть L =
{R} состоит из одного предикатного символа, и пусть #(R) = 2. Модель языка
L задаётся как пара A = (A, r), состоящая из множества А и
отношения r Н A2, равного RA.
Такую модель можно представить как ориентированный граф, вершинами
которого являются элементы из А, а рёбрами - пары (a, b) О
r . Произвольное множество с отношением порядка будет моделью
этого языка, если положить RA = (Ј).
Пример
2
Полугруппой называется множество А вместе с бинарной операцией
Ч : A2 ® A, удовлетворяющей закону
ассоциативности a Ч (b Ч c) = (a Ч b)
Ч c, для всех a, b, c О A. Полугруппа вместе с элементом
e О A, удовлетворяющим для всех a О A соотношениям e
Ч a = a Ч e = a, называется моноидом. Моноид, в котором
для каждого a О A задан такой элемент a -1 О
A, что a Ч a -1 = a -1 Ч a = e,
называется группой. Язык теории полугрупп L = {Ч} состоит из
одного элемента, #(Ч) = 2. Язык теории моноидов L = { Ч,
e} состоит из символов бинарной операции и константы. Язык теории групп L
= {Ч, () -1, e} состоит из символов бинарной и унарной
операций и из символа константы. Множество действительных чисел R вместе с
аддитивными операциями (R, +, -x, 0) будет моделью языка теории групп.
Символы интерпретируются следующим образом:
Ч R =
+; (() -1)R = -; eR = 0.
Моделью языка
теории групп будет также множество R + положительных
действительных чисел с мультипликативными операциями 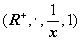 .
Множество натуральных чисел w можно рассматривать как линейно
упорядоченный моноид, если определить язык теории линейно упорядоченных
моноидов как L = {+, 0, Ј}. .
Множество натуральных чисел w можно рассматривать как линейно
упорядоченный моноид, если определить язык теории линейно упорядоченных
моноидов как L = {+, 0, Ј}.
Модели языка теории групп могут не
удовлетворять закону ассоциативности и другим формулам, определяющим
группу. Наша задача - дать формальное определение истинности предложений
q в модели А языка первого порядка. Будем записывать выполнение
формулы q в модели А, как А |= q. Например:
(R, +, 0)
|= "x $y (x Ч y = e)
будет верно, поскольку
для каждого a О R существует такой b О R, что a + b =
0.
Обычно не для всякого элемента модели существует символ константы,
обозначающий этот элемент. Предположим, однако, что для каждого a
О A существует такой символ константы ca в языке L,
что caA = a. Интерпретацию операций можно расширить
на термы, не содержащие переменных, с помощью преобразования:
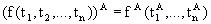 . .
Каждому терму t без переменных будет соответствовать
элемент tA О A. Определим отношение |= (“удовлетворяет
формуле”) по индукции:
1) A |= R(t1, t2, ...,
tn), если (t1A, ...,
tnA) О RA
2) A |=
Шq, если и только если утверждение A |= q ложно;
3) A
|= (q Ъ y), если и только если A |= q
или A |= y;
4) A |= $x q(x), если и только
если существует такой b О A, что A |=
q(cb).
Определим теперь A |= q для
произвольных языка L и модели А этого языка. Пусть LA = L
И (ca : a О A), где ca - символы
констант. Обозначим через (A, a)a О A модель языка
LA, полученную из модели A сопоставлением каждому ca
О LA элемента a.
Заметим, что поскольку
"x q(x) равносильно Ш$x (Шq(x)), то A
|= "x q(x) тогда и только тогда, когда для всех b
О A верно A |= q (cb).
Если q -
предложение языка L, то положим: A |= q, если и только если (A,
a)a О A |= q.
Пример 3
Пусть L = {
Ч, e, R} - язык теории частично упорядоченных моноидов.
Рассмотрим модель N = (w , +, 0, Ј). Справедливость
утверждения:
( w , +, 0, Ј) |=
"x0 "x1
"x2(R(x0, x1) ®
R(x0 Ч x2, x1 Ч
x2))
равносильна выполнению стоящего в правой части
равенства предложения для модели (N, n)n О w
языка LN = {Ч, e, R} И {cn : n
О w}. Предложение означает, что для любых p, q, r
О w верно R(cp, cq) ®
R(cp Ч cr, cp Ч
cr), интерпретируемое как p Ј q ® p + r
Ј q + r.
Замечание. Альфред Тарский был первым, ясно
осознавшим необходимость определения истинности предложения для модели. Он
предложил следующий метод, отличный от рассматриваемого нами.
Пусть А -
модель языка первого порядка L. Рассмотрим произвольную функцию b
: w ® A. Будем называть её А-оценкой и представлять в
виде бесконечной последовательности b = (b0,
b1, b2, ...), i-й член которой является значением
переменной xi, даваемой оценкой b. Определяется оценка
b(t) для каждого терма:
1) если t есть переменная
xi, то b(t) = bi;
2) если t есть
константа с, то b(t) = cA;
3) если t есть n-арная
операция, то b(f(t1, ... , t2)) = f
A( b(t1), ...,
b(t2)).
Выполнение формулы q в модели А
при оценке b записывается как A |= q[ b] и
определяется по индукции:
1) A |= R(t1, ... ,
tn)[ b], если и только если ((
b(t1), ..., b(tn)) О
R A);
2) A |= Шq[b], если и только если A
|= q[ b] ложно;
3) A |= (q Ъ
y)[ b], если и только если A |= q[b]
или A |= q[ y].
4) A |= $x1
q(x1)[ b], если и только если q
выполнена хотя бы на одной последовательности b' =
(b0, b1, ..., bi-1, a, bi+1,
...), отличной от b не более чем в одной i-й
компоненте
Наконец, модель А называется удовлетворяющей формуле
q, если A |= q[ b] для всякой оценки
b.
Возвращаясь к нашему первоначальному определению, отметим
следующее утверждение, доказательство которого ясное, но
громоздкое:
Пусть L1 Н L2 - языки
первого порядка. Для любой модели А языка L1 обозначим через
A|L1 множество А, рассматриваемое как модель языка
L1. Тогда для любого предложения q языка L1
утверждение A |= q истинно, если и только если
A|L1 |= q.
|
|
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
4. Модели теории первого порядка
Среди моделей языка первого порядка выделяются модели, удовлетворяющие
набору аксиом. Этот набор и будет определять теорию, а модели, для которых
выполнены аксиомы, будут моделями теории.
Теорией (первого порядка) Т в
языке L называется произвольное множество предложений языка L.
Таким
образом, теория получается из исчисления предикатов добавлением некоторого
множества предложений T.
Моделью теории Т называется модель А языка L,
такая, что A |= q для всех q О Т. Теория Т
непротиворечива, если она состоит из непротиворечивого множества
предложений. Если существует модель теории Т, то Т называется выполнимой.
Множеством аксиом теории Т называется всякое её подмножество е
Н Т такое, что для каждого предложения q О Т
существует вывод е 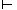 q .
Если существует конечное множество аксиом, то Т называется конечно
аксиоматизируемой. q .
Если существует конечное множество аксиом, то Т называется конечно
аксиоматизируемой.
Рассмотрим теории наиболее часто встречающихся
моделей.
Теория частично упорядоченных множеств
Язык L = {
Ј} состоит из одного двухместного предиката. Теория имеет 3
аксиомы:
1) "x "y "z (x Ј y & y
Ј z ® x Ј z);
2) "x "y (x
Ј y & y Ј x ® x = y);
3) "x (x
Ј x);
Моделями этой теории являются частично упорядоченные
множества. Если присоединить аксиому:
4) "x "y (x
Ј y Ъ y Ј x),
то получим теорию, моделями
которой служат линейно упорядоченные множества.
Теория булевых алгебр
Язык L = { З, И, Ш} состоит из символов
двух бинарных операций и одной унарной. Теория имеет аксиомы 1 - 6 (разд.
1.11) (все свободные переменные в этих аксиомах превращены в связанные с
помощью кванторов всеобщности). Моделями будут булевы алгебры.
Теория
групп
Пусть L = {Ч, () -1, e} состоит из символов
бинарной и унарной операций и константы. Теория групп определяется
аксиомами:
1) "x "y "z (x Ч (y
Ч z) = (x Ч y) Ч z);
2) "x (e
Ч x = x & x Ч e = x);
3) "x (x
Ч x -1 = e & x -1 Ч x =
e).
Моделями служат группы. Если добавить аксиому
коммутативности:
4) "x "y (x Ч y = y
Ч x),
то получим теорию, моделями которой являются абелевы
группы.
Теория чисел
Пусть L = {+, Ч, S, 0} состоит из двух
бинарных операций + и Ч, унарной операции S и символа константы
0. Теория чисел задаётся аксиомами Пеано:
1) "x (Ш(0
= Sx));
2) "x "y (Sx = Sy ® x = y);
3) x
+ 0 = x;
4) x + Sy = S(x + y);
5) x Ч 0 = 0;
6) x
Ч Sy = (x Ч y) + x;
7) "x1 ...
"xn( q(0, x1, ..., xn)
& "x0 q(x0, x1,
..., xn) ®
® q(Sx0,
x1, ..., xn)) ® "x0
q(x0, x1, ..., xn)) для каждой
формулы q , не содержащей связанных вхождений
x0.
Аксиома 7 (аксиома индукции) состоит в действительности
из бесконечного числа предложений, каждое из которых соответствует
некоторой формуле q языка L.
Стандартной моделью теории чисел
является модель ( w, +, Ч, S, 0) с обычными операциями
сложения и умножения чисел. Операция S интерпретируется как функция S(x) =
x + 1. Существуют и нестандартные модели теории чисел.
Теория множеств
Пусть L = { О}. Добавим логическую связку q
« y, служащую сокращением для (q ®
y) & ( y ® q). Запишем в виде
формул аксиомы Цермело-Френкеля (разд. 1.2). Эти аксиомы определяют теорию
ZF:
1) $x "y (Ш(y О x)) (пустое
множество);
2) "x "y "z ((z О x
« z О y) ® (x = y))
(экстенсиональность);
3) "u "v $x
"z (z О x « z = u Ъ z = v)
(пара);
4) "x $y "z "u (u
О z & z О x ® u О y)
(объединение);
5) "x $y "u ("v (v
О u ® v О x) ® u О y)
(множество подмножеств);
6) $x ($y (y О x)
& "y (y О x ® $z (y О z
& z О x))) (бесконечность);
7) "x1 ...
"xn "v $w "u (u О
w « u О v & q(u, x1, ...,
xn) (схема аксиом выделения);
8) "u
"x1 ... "xn( "x
$!z q(x, z, u, x1, ..., xn)
®
® $y "z (z О y
« $x (x О u & q(x, z, u,
x1, ..., xn)) (схема аксиом подстановки);
9)
"u $x (x О u & "v (Ш(v
О x & v О u))) (регулярность).
Если добавить к
этой системе аксиом аксиому выбора, то получится теория ZFC. Существуют
различные модели теории множеств. Далее мы увидим, что существуют модели,
в которых число всех множеств счётно.
|
|
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
5. Компактность и полнота языка первого порядка
Теорема компактности для счётных языков была доказана Куртом Гёделем в
1930 году. Анатолий Иванович Мальцев доказал её для произвольных языков
первого порядка в 1936 году. Мы будем следовать доказательству Генкина
(1949 г.).
Напомним, что теории - это множества предложений. Множество
предложений е языка L называется конечно выполнимым, если каждое
конечное подмножество из е имеет модель. Множество е -
полное, если для каждого предложения q либо q О
е , либо Шq О е.
Лемма 1. Для
каждого конечно выполнимого множества е предложений языка первого
порядка существует полное конечно выполнимое множество предложений
е' К е.
Доказательство. Пусть B = {Q : Q
К е и Q - конечно выполнимо}. Легко видеть, что (B,
Н) удовлетворяет лемме Куратовского-Цорна. Значит, существует
максимальное конечно выполнимое е' К е. Для
каждого предложения q либо е' И {q},
либо е' И { Шq} конечно выполнимо. В противном
случае существуют конечные F0, F1 Н
е' такие, что F0 И { q} и
F1 И {Шq} не имеют моделей, хотя
F0 И F1 будет иметь некоторую модель А в
силу конечной выполнимости е. Для этой модели либо A |=
q , либо A |= Шq. Противоречие показывает, что либо
q О е', либо Шq О
е'. Следовательно, е' - полное.
Лемма 2. Если
е - конечно выполнимое множество предложений языка L с одной
свободной переменной x, а с - новый символ константы (не принадлежащий L),
то е И {( $x q(x)) ®
q(c)} - конечно выполнимо в языке L И
{с}.
Доказательство. Новое предложение ($x q(x))
® q(c) называется предложением Генкина, а константа с -
константой Генкина. Предположим, что е И {($x
q(x)) ® q(c)} не является конечно выполнимым.
Тогда существует конечное F Н е, такое, что F И
{($x q(x)) ® q(c)} не имеет модели.
Пусть А - модель языка L, удовлетворяющая F. Так как константа с не
принадлежит L, то мы можем интерпретировать её произвольным образом. Если
A |= $x q(x), то существует b О А, для которого
A |= q(cb). В этом случае, сопоставляя символу с
элемент b, мы расширим модель на L И {c}. Получим A |=
q(c), а вместе с тем A |= $x q(x) ®
q(c). Если же $x q(x) ложно в модели А, то
символу c можно сопоставить любой элемент из А. Во всех случаях модель А
будет удовлетворять F И {( $x q(x)) ®
q(c)}.
Определение. Множество е предложений языка L
называется множеством Генкина, если для каждой формулы q(x) с
единственной свободной переменной х существует такой символ константы с
О L, что
(( $x q(x)) ®
q(c)) О е.
Лемма 3. Если е -
конечно выполнимое множество предложений языка L, то существуют такие
е' К е и L' К L, что е'
является конечно выполнимым множеством Генкина предложений языка
L'.
Доказательство. Для любого множества a предложений языка L
положим: е* = е И {$x q(x)
® q (cq) : q(x) - формула
языка L с одной свободной переменной}. Язык теории е* содержит
новый символ константы c q для каждой формулы
q(x). Применяя к конечным подмножествам теории е* лемму
2, получим конечную выполнимость множества е*. Далее положим:
е0 = е и еm+1 =
еm* для всех m О w. Тогда множество
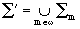 будет множеством Генкина. Оно конечно выполнимо как
объединение цепи конечно выполнимых множеств. будет множеством Генкина. Оно конечно выполнимо как
объединение цепи конечно выполнимых множеств.
Каноническая модель
теории
Пусть е - множество предложений языка L. Канонической
моделью А теории е называется модель, построенная следующим
образом:
1) обозначим через Y - множество всех термов языка L, не
содержащих переменных;
2) для t1, t2 О Y
определим t1 ~ t2, если и только если
(t1 = t2) О е;
3) предполагая,
что ~ - отношение эквивалентности, обозначим через [t] класс
эквивалентности терма t О Y;
4) универсум модели А определим
как множество классов эквивалентности относительно отношения
~;
5) для любого символа константы положим сА =
[с];
6) для любой n-арной операции f положим
fA([t1], …, [tn]) = [f(t1, …,
tn)];
7) для любого символа предиката R
положим:
([t1], …, [tn]) О
RA, если R(t1, …, tn) О
е.
Лемма 4. Если е - конечно выполнимое полное
множество Генкина предложений языка L, то каноническая модель А для
е определена корректно, и для каждого предложения q
языка L верно, что A |= q тогда и только тогда, когда q
О е.
Доказательство состоит из проверки того, что
~ - отношение эквивалентности, перестановочное с символами
операций и отношений. Сформулированное свойство доказывается по
индукции.
Теорема (о компактности). Для произвольных языка L и
множества е предложений языка L, если каждое конечное
подмножество из е имеет модель, то е имеет модель.
Доказательство. По лемме 3 существует конечно выполнимое множество
Генкина: е' И е . Возьмём его пополнение,
существующее по лемме 1. Рассмотрим каноническую модель полученной теории.
Ограничение этой теории на е будет искомой моделью на
е.
Лемма 5. Мощность множества формул языка L равна
max(|L|, |w|).
Теорема (Лёвенгейма-Скулема). Если теория Т
языка L имеет модель, то она имеет некоторую модель мощности, не большей
max(|L|, | w|).
Доказательство. Каноническая модель пополнения
множества Генкина Т ', построенного для Т, имеет мощность Ј
max(|L|, |w|).
Из этой теоремы, в частности, вытекает, что
существуют счетные модели теории множеств. Имеет место и теорема
Лёвенгейма-Скулема о существовании моделей большой мощности. Она
утверждает, что для любой модели А языка L существует содержащая её модель
B произвольной мощности B Ј max(|A|, |L|). В частности,
существуют несчетные модели теории натуральных чисел.
Полнота теории
первого порядка
Кроме исчисления предикатов существуют другие
формальные теории, связанные с языком первого порядка. Мы рассмотрим
исчисление предикатов. Наиболее простая из них - исчисление ММ. Логические
аксиомы в этой системе - предложения q, истинные в любой модели
языка первого порядка L. Правило вывода одно - Modus Ponens. Мы будем
опираться далее на равносильность этой формальной теории исчислению
предикатов, которая в действительности вытекает из теоремы Гёделя о
полноте исчисления предикатов.
Теорема о полноте теории первого
порядка. Пусть заданы произвольные множества предложений a и
предложение q языка L. Вывод е 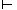 q
существует тогда и только тогда, когда каждая модель теории е
удовлетворяет предложению q. q
существует тогда и только тогда, когда каждая модель теории е
удовлетворяет предложению q.
Доказательство. В случае
е 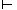 q и A |= q доказывается очевидным образом с
помощью индукции по длине вывода е q и A |= q доказывается очевидным образом с
помощью индукции по длине вывода е 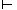 q
(теорема о корректности). Пусть, наоборот, каждая модель A |= е
удовлетворяет q. Так как всякая модель е является
моделью для q, то множество предложений е И
{Шq} не имеет моделей. По теореме компактности существует такое
конечное подмножество { q1, …, qn}
Н е, что { q1, …,
qn, Шq} не имеет моделей. Отсюда
Ш(q1 & … & qn
& Шq) - тавтология исчисления ММ. Значит, имеет место
логическая аксиома: q1 ®
(q2 ® (… ® (qn
® q) …))), из которой будет вытекать вывод: е q
(теорема о корректности). Пусть, наоборот, каждая модель A |= е
удовлетворяет q. Так как всякая модель е является
моделью для q, то множество предложений е И
{Шq} не имеет моделей. По теореме компактности существует такое
конечное подмножество { q1, …, qn}
Н е, что { q1, …,
qn, Шq} не имеет моделей. Отсюда
Ш(q1 & … & qn
& Шq) - тавтология исчисления ММ. Значит, имеет место
логическая аксиома: q1 ®
(q2 ® (… ® (qn
® q) …))), из которой будет вытекать вывод: е
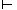 q. q.
Теги:Термы. Предикаты. Унификация. Исчисление высказываний.
Семантика. Семантика языка. Теория групп. Робинсон. Метод
резолюций.
|
|
|

 Выход
Выход q
означает, что существует вывод формулы q из логических аксиом и
формул из множества е. Если Ж
q
означает, что существует вывод формулы q из логических аксиом и
формул из множества е. Если Ж