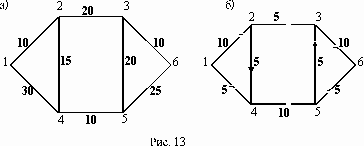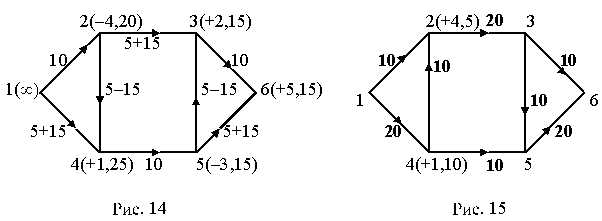Решение типовых задач по графам - Е.Л Рабкин, Ю.Б. Фарфоровская ДИСКРЕТНАЯ МАТЕМАТИКА
| Добавил: | DMT |
| Дата создания: | 4 мая 2008, 1:05 |
| Дата обновления: | 4 мая 2008, 1:11 |
| Просмотров: | 23064 последний --- |
| Комментариев: | 0 |
Решение типовых задач по графамТребуется по данному ориентированному графу составить структурную матрицу, а по ней (методами булевой алгебры) найти все пути из вершины i в вершину j, а затем (отрицанием этих путей) найти все сечения между двумя указанными вершинами. Пусть дан ориентированный граф (рис. 12) , причем ребра a,b,h являются ориентированными (их на правление указано стрелками), а остальные ребра не ориентированы. Требуется методами булевой алгебры найти пути и сечения между вершинами 2 и 4.
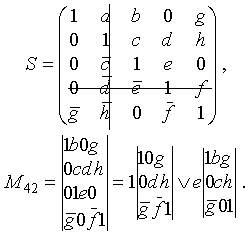
Составляем структурную матрицу S, затем вычеркиваем из нее 4-ю строчку и 2-й столбец (тем самым получаем минор М(4,2)):
Раскрытие определителей производится по известному правилу: определитель равен сумме (в данном случае дизъюнкции) произведений элементов, умноженных на свои алгебраические дополнения (в данном случае просто миноры). При этом для определителей 3-го порядка можно пользоваться и правилом треугольника. Тогда получаем
Искомые пути, расположенные в порядке прохождения ребер: П 24 = d ЪhfЪ ceЪ hgbe. Сечения же получатся отрицанием этих путей. Применяя правила де Моргана (заменяя конъюнкцию на дизъюнкцию и наоборот), затем раскрывая скобки, получаем: (знаки отрицания опущены во всех равенствах, кроме 1-го):
S24= d(hЪ f)(e Ъch Ъcg Ъcb) = d(he Ъch Ъcgh ЪсbhЪfe fЪchЪfcg Ъfcb), или, применяя в скобках правило поглощения, получаемЪ S24 = d(heЪ ch Ъfe fЪcg Ъfcb), S24=dheЪdch Ъdfе Ъdfcg Ъdfcb.
Требуется найти в данной сети (т. е. в графе с заданными пропускными способностями ребер) максимальный поток из вершины с номером 1 в вершину с наибольшим номером (в заданиях либо в вершину 5, либо 6). В заданиях заданы 2 графа (граф, который находится слева, – это сеть с заданными пропускными способностями ребер, и граф справа с заданным потоком, который необходимо либо улучшить, либо доказать, что он не улучшаем и, значит, является максимальным). Конечно, можно дать задание просто найти максимальный поток между двумя вершинами. Однако при работе вручную нельзя дать большое число вершин (в наших заданиях это число равно 5 или 6), а в этих случаях максимальный поток можно найти без всякой теоремы Форда-Фалкерсона (просто из общих соображений). Поэтому задание в примерах 61–70 состоит в том, чтобы правильно расставить пометки для заданного потока, указанного в графе справа и после этого делать выводы о том, является ли этот поток максимальным или нет. Требуется, расставляя пометки в графе с заданным потоком с помощью алгоритма, описанного в теореме Форда – Фалкерсона, найти максимальный поток между вершиной с номером 1 и вершиной с максимальным номером. При этом если улучшенный поток окажется максимальным, то нужно указать то минимальное сечение, которому равен наш поток (если же улучшенный поток не окажется максимальным, то нужно снова его улучшать до тех пор, пока он не окажется максимальным). На рис. 13а изображен граф с данными пропускными способностями ребер, при этом вершина номер 1 является “источником”, а вершина 6 – стоком. На рис. 13б изображен тот же граф, но на ребрах его задан поток, удовлетворяющий свойствам 1–4, который надо либо увеличить, либо доказать, что он является максимальным.
После этого подробно объясняем, как расставляются пометки в этом графе, и результат этого показываем на рис. 14. Для нового потока (рис. 14) снова расставляем пометки и убеждаемся, что этот поток является максимальным (рис. 15). Здесь же находим минимальное сечение, которому равен поток. Начинаем расставлять пометки во втором графе (там дан поток).
Это означает, что дуга (4,2) обратная, и, учитывая возможный “разворот” ее, по ней можно дополнительно “перевезти” 20 единиц “груза”. Так как 20 меньше 25, получаем данную пометку. Теперь можно пометить вершину 3 пометкой (+2,15) и, вершину 5, пометка которой будет (–3,15). (Заметим, что по дуге (5,3) с учетом разворота можно дополнительно “перевезти” 25 единиц груза, но так как для вершины 3 второе число было равно 15, то любое следующее число не может быть его больше). Только после этого можем пометить вершину 6 (сток), пометка которой будет (+5,15). Таким образом, наш поток можно увеличить на 15 единиц, прибавляя эти 15 единиц к прямым дугам и вычитая из обратных с учетом возможного “разворота” обратных дуг. Результат всех этих действий изображен на рис. 14. Таким образом, получили новый поток, изображенный на рис. 15. После этого для нового потока (рис. 15), снова расставляем пометки, которые также изображены на рис. 15. Мы видим, что для этого потока (кроме источника) можно пометить только 2 вершины: вершину 4 (ее пометка будет (+1,10)) и (после этого) вершину 2, пометка которой будет (+4,5). Больше ничего пометить нельзя, так как из множества помеченных вершин (Y) в множество непомеченных вершин (Z) идут только прямые, насыщенные дуги (дуги (2–3) и (4–5)). Эти две дуги образуют минимальное сечение, величина которого равна 30 условных единиц, и эта же величина равна величине потока. Заметим, что величина потока также равна “количеству груза”, вывозимого из источника, и равна количеству груза, ввозимого в сток. Таким образом, поток на рис. 15 является максимальным, а дуги (2–3) и (4–5) образуют минимальное сечение, которому равен наш поток. | |

 Выход
Выход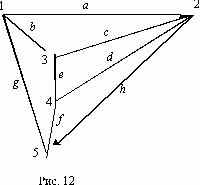
 .
.