Эйлеровы и полуэйлеровы графы - Е.Л Рабкин, Ю.Б. Фарфоровская ДИСКРЕТНАЯ МАТЕМАТИКА
| Добавил: | DMT |
| Дата создания: | 4 мая 2008, 0:48 |
| Дата обновления: | 4 мая 2008, 0:49 |
| Просмотров: | 13680 последний --- |
| Комментариев: | 0 |
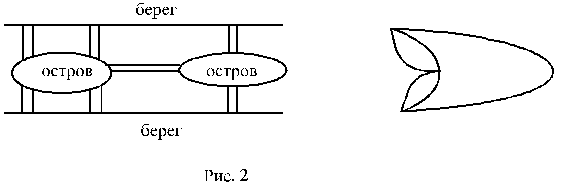
Эйлеровы и полуэйлеровы графыИменно с задач, поставленных и решенных в этом разделе, началась теория графов. Философ Иммануил Кант, гуляя по городу Кенигсбергу (сейчас этот город называется Калининград), поставил задачу (1736), известную в математике как задача о семи кенигсбергских мостах: можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. Наш петербургский знаменитый математик швейцарского происхождения Леонард Эйлер блестяще решил эту задачу. На рис. 2 изображена схема семи мостов Кенигсберга (заметим, что сейчас осталось только два из них), а также мультиграф, соответствующий этой схеме (при построении графа считалось, что каждый берег реки и острова – это вершины графа, а мосты – его ребра; видно, что в данном случае у нас получился мультиграф без петель).
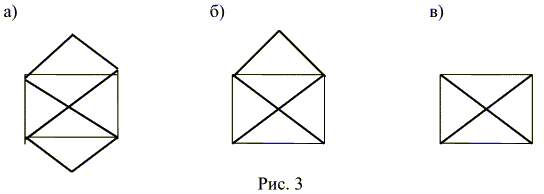
В соответствии с поставленной Кантом (и решенной Эйлером) задачей можно дать следующие определения: Граф (или мультиграф без петель) называется эйлеровым, если существует цикл без повторения ребер (такой цикл называют эйлеровым), обходящий все вершины графа. Граф называется полуэйлеровым, если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз. На рис. 3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым (люди старшего поколения знают, что в школах раньше было много загадок типа “можно ли нарисовать данную фигуру не отрывая ручку от бумаги”, что и соответствует эйлерову или полуэйлерову графу).
Теорема (Эйлер). Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными.Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными. Доказательство этой теоремы начнем с так называемой леммы о рукопожатиях. Название этой леммы связано с тем, что эта лемма отвечает на следующий вопрос: У Вас собрались гости. Некоторые из них здороваются друг с другом посредством рукопожатий. Какими свойствами обладает число таких людей? Ответ дается следующей достаточно простой леммой. Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно. Доказательство леммы. Заметим, что сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной. Это следует из того, что если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю. Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы. Таким образом, сумма всех степеней вершин четна. Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной. Это значит, что само число таких вершин должно быть четным. Лемма доказана. С точки зрения задачи о рукопожатиях это означает, что число гостей, которые поздоровались за руку нечетное число раз, должно быть четным.Перейдем к доказательству теоремы Эйлера. А) Пусть граф является эйлеровым. Тогда в нем имеется эйлеров цикл, который должен прийти в вершину по одному ребру и покинуть его по другому, так как каждое ребро должно использоваться только один раз (т. е. каждый “заход” в вершину и “выход” из нее дает 2 степени вершины). Таким образом, сумма степеней всех вершин должна быть четной (и равна удвоенному числу “заходов” в эту вершину при обходе эйлерова цикла). Б) Пусть в данном связном графе (или мультиграфе без петель) степень любой вершины четна (т. е. степень больше или равна 2, так как нулевая степень приводит к несвязному графу). Докажем, что в нем имеется эйлеров цикл. Доказательство проведем индукцией по числу вершин. В случае, когда в связном графе всего 2 вершины и обе они имеют четную степень (в этом случае имеем мультиграф, один из которых изображен на рис. 4), ясно, что в этом случае имеется эйлеров цикл (при любой четной степени этих двух вершин).
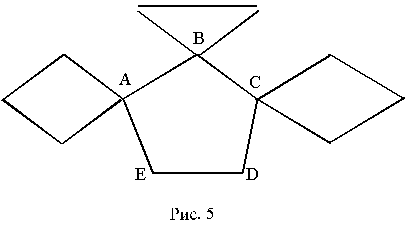
Предположим, что наше утверждение верно для всех связных графов, число вершин в которых строго меньше п, и докажем его для графа, имеющего п вершин. Заметим, что по лемме 1 в этом графе есть контур (степень всех вершин больше или равна 2). Если этот контур содержит все ребра, то этот контур сам является эйлеровым циклом (а граф эйлеровым). Удалим все эти ребра из графа и те вершины, которые после удаления ребер стали иметь нулевую степень. Тогда получим новый граф (который может быть несвязным), но в этом новом графе все вершины обязательно имеют четную степень (так как при удалении ребер контура степень каждой вершины, входящей в этот контур, уменьшается на 2). Новый граф распадается на “компоненты связности”, каждая из которых должна иметь общую вершину с удаленным контуром (иначе первоначальный граф не был бы связным), степени всех вершин каждой компоненты связности четны и число вершин в ней строго меньше п, т. е. по индукционному предположению эта компонента имеет эйлеров цикл. Теперь можем построить эйлеров цикл в данном графе следующим образом. Обходим последовательно ребра удаленного контура. Если мы пришли в вершину, общую для контура и какой-то компоненты связности, то обходим по эйлерову циклу эту компоненту, возвращаемся при этом в вершину контура и идем по этому контуру дальше. Тем самым все ребра будут пройдены и каждое только один раз (все это схематично изображено на рис. 5: сначала начинаем обходить контур АВСDEА. Пройдя ребро АВ, проходим “верхний” граф, затем возвращаемся в т. В и далее идем по ребру АС, обходим “правый” граф и т. д.). Утверждение Б доказано.
В) Пусть теперь граф полуэйлеров. Это значит, что он имеет эйлеров путь, начинающийся в одной вершине и заканчивающийся в другой. Видно, что обе эти вершины должны иметь нечетную степень, а степень остальных четная. Г) Обратно. Пусть в связном графе вершины к и р имеют нечетную степень, а остальные вершины – четную. Тогда возможны 2 случая: эти вершины связаны ребром или не связаны. В первом случае удалим это ребро, а во втором добавим. В обоих случаях степень всех вершин станет четной. Заметим, что в случае удаления ребра, новый граф может стать несвязным и иметь 2 компоненты связности (в этом случае удаляемое ребро было мостом), каждая из которых или весь новый граф имеет эйлеров цикл. Теперь если новый граф имеет эйлеров цикл, то начнем (и закончим его) в вершине с нечетной степенью и далее добавим ребро или удалим его. В обоих случаях получим эйлеров путь. Если новый граф имеет 2 компоненты связности, то, пройдя одну из них по эйлерову циклу, начиная и заканчивая в вершине (которая в первоначальном графе имела нечетную степень), затем добавим удаленное ребро (мост), пройдем его, попадем в другую вершину, которая ранее имела нечетную степень, и пройдем вторую компоненту связности по эйлерову циклу. Во всех разобранных случаях получим эйлеров путь, который начался в одной из вершин с нечетной степенью и закончился в другой. Теорема доказана. Заметим, что все 4 вершины мультиграфа (рис. 2), соответствующего мостам Кенигсберга, имеют степень 3. Поэтому эйлеров цикл или путь невозможен. Примечание. Если граф (или мультиграф без петель) содержит 2k вершин нечетной степени, то его можно разбить на k полуэйлеровых графов (т. е. нарисовать k росчерками пера). Доказательство аналогично доказательству теоремы Эйлера. Имеется простой алгоритм (так называемый алгоритм Флери) для нахождения эйлерова цикла (конечно, если этот цикл существует), который состоит в следующем: начинаем с любой вершины и “стираем” пройденные ребра. При этом по мосту (перешейку) проходим только, если нет других возможностей. Очевидно, что для того чтобы построить эйлеров путь достаточно использовать алгоритм Флери, который надо начать с вершины, имеющей нечетную степень. Рассмотрим некоторые приложения теоремы Эйлера, которые в основном связаны с так называемой задачей китайского почтальона. Пусть имеется некоторый граф (связный), ребрам которого приписаны некоторые числа, называемые весами ребер (часто, но не всегда!, в приложениях вес ребра – это его длина). Требуется найти такой цикл, при котором каждое ребро проходится по крайней мере один раз и суммарный вес всех ребер, вошедших в цикл, минимален. Заметим, что если граф является эйлеровым, то любой эйлеров цикл решает поставленную задачу (для эйлерова графа веса роли не играют). Эта задача имеет много приложений, например, поливка улиц одной машиной (здесь ребра графа – дороги, а перекрестки – вершины; веса – это длины дорог), а также сбор мусора, доставка почты или даже наилучший маршрут для осмотра музея или уборка помещений и коридоров в больших учреждениях. Заметим, что имеется алгоритм решения задачи китайского почтальона, но он требует достаточно длительного описания. Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном (связном) графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут – путем), то граф называется гамильтоновым (полугамильтоновым), и соответствующий цикл (путь) также называют гамильтоновым циклом (путем). На рис. 6 изображены гамильтонов, полугамильтонов и не гамильтонов графы.
Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, “хорошего” решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном – это теоремы типа “если в графе достаточное число ребер, то он гамильтонов”. Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, (рис. 6,а), поскольку в графах такого типа вершин может быть очень много, а ребер сравнительно мало). Приведем без доказательства самую известную теорему. Теорема (Дирак, 1952). Если в связном графе с п вершинами (при nі3) степени всех вершин больше или равны п/2, то граф гамильтонов. | |

 Выход
Выход