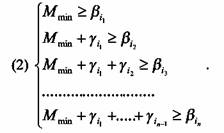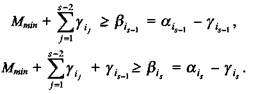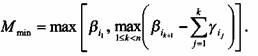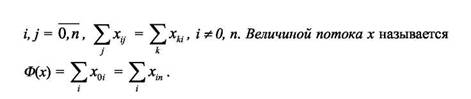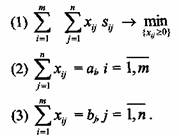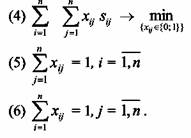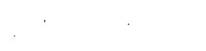Псевдопотенциальные графы - В.Н. Бурков, Д.А. Новиков ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
| Добавил: | DMT | |||||||
| Дата создания: | 4 мая 2008, 0:38 | |||||||
| Дата обновления: | 4 мая 2008, 0:50 | |||||||
| Просмотров: | 11174 последний --- | |||||||
| Комментариев: | 0 | |||||||
|
3. Псевдопотенциальные графы Полный, (я+7)-вершинный, симметричный граф называется
псевдопотенциальным, если длина его любого гамильтонова кон тура
равна одному и тому же числу. Обозначим Известно [7, 8], что для того, чтобы граф был псевдопотенци альным,
необходимо и достаточно существование чисел
любой подграф псевдопотенциального графа является псевдопо тенциальным. Будем считать, что ао = 0. Обозначим - сумма длин первых j дуг гамильтонова контура Известно [7, 8], что существует оптимальное решение задачи
в котором сначала идут вершины величин
Для доказательства этого утверждения обозначим
нов контур (решение задачи (1)). Тогда для него имеет место сле дующая система неравенств:
Если для некоторого индекса
Если ливость соответствующей системы неравенств для гамильтонова контура Наконец, если справедливость соответствующей системы неравенств для гамиль тонова
контура
Итак, пусть нием задачи (1), то есть
Тогда (3) Частным случаем псевдопотенциального графа является по тенциальный граф, у которого длина любого гамильтонова конту ра равна нулю 1 . В частности, потенциальный граф обладает сле ду 4fa ющими свойствами: • у потенциального графа длина любого контура равна нулю; • для я-вершинного потенциального графа существуют числа
- у потенциального графа для любой вершины сумма длин за 4. Задачи о максимальном потоке Рассмотрим сеть из ( n + 1) вершины. Пусть каждой дуге поставлено в соответствие число cij , называемое пропускной способностью дуги ( i ; j ). Потоком x в сети называется совокупность чисел
Задача о максимальном потоке заключается в определении потока максимальной величины 1 . Разрезом W в сети называется любое множество вершин, обя зательно содержащее выход и не содержащее вход. Пропускной способностью C ( W ) разреза W называется сумма пропускных способностей дуг, заходящих в разрез. Известно [5, 7, 19], что величина любого потока не превышает пропускной способности любого разреза {теорема Форда- Фалкерсона ). Следовательно, если удастся найти поток, величина которого равна пропускной способности некоторого разреза, то этот поток максимален, а разрез минимален. Алгоритм 7 (алгоритм Форда-Фалкерсона ). Применение алго ритма проиллюстрируем примером сети, приведенной на рисунке 3, в которой пропускные способности всех дуг равны единице. Шаг 0. Берем произвольный поток (например, поток x01 = Хп = x25 = 1). Помечаем начальную вершину индексом «0». Обозначим Z - множество помеченных вершин. Общий шаг. Первое действие. Помечаем вершину j индексом
+ i , если, во-первых, существует дуга (
i ; j ), и, во-вторых, Если
Рис. 3. Пои 513 ск максимального потока Второе действие. Помечаем вершину i индексом -
j , если, во-первых, существует дуга ( j ; i ), и,
во-вторых, Если в результате этого типа пометок мы пометили выход, то поток можно увеличить. Двигаясь обратно, можно найти цепь, в которой каждая вершина помечена номером предыдущей (знак пометки не важен). Рассмотрим цепь \ i = (0; 3; 2; 1; 4; 5), приведенную на рисунке 3. Полученные в результате второго действия потоки обозначе ны жирным шрифтом. Критерий остановки алгоритма следующий [7, 8]: если, применяя пометки обоих типов, вершину n пометить не удалось, то полученный поток имеет максимальную величину. Поток минимальной стоимости. Предположим, что задана сеть с
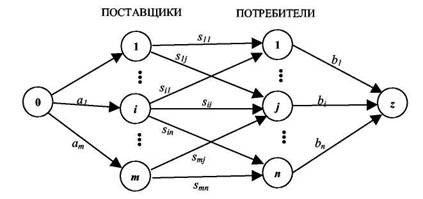
пропускными способностями дуг Частным случаем задачи о потоке минимальной стоимости является транспортная задача, в которой имеется двудольный граф (двудольным называется граф, множество вершин которого может быть разбито на два непересекающихся подмножества, причем ребра ( дуги) графа соединяют вершины только из разных подмножеств), представленный на рисунке 4: вершины сети разбиты на две группы - m поставщиков и n потребителей. Известно [15], что граф является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины, или когда в нем все простые циклы имеют четную длину {теорема Кенига). Для поставщиков заданы имеющиеся у них количества единиц товара (груза и
532
т.д.) а*, количества единиц товара перевозки единицы товара от г-го поставщика у '- му потребителю. Пусть задача является замкнутой, то есть
ное предложение равно суммарному спросу (вводя фиктивного поставщика или фиктивного потребителя любую незамкнутую задачу можно свести к замкнутой ). Требуется определить потоки товаров от потребителей к поставщикам, минимизирующие сум марные затраты.
Формально транспортную задачу можно записать в виде:
Добавляя к двудольному графу вход «0» и выход « z » и соеди няя вход и выход с остальными вершинами дугами с потоком
Частным случаем транспортной задачи является задача о на
значении, заключающаяся в следующем:
имеются n человек (работников), которые могут выполнять
различные работы (занимать различные должности), число работ равно числу
работников (введя фиктивные должности и/или фиктивные работы, всегда можно
незамкнутую задачу привести к рассматриваемой замкнутой фор ме). Известны
затраты Формально задачу о назначении можно записать в виде (ср. с (1)-(3)):
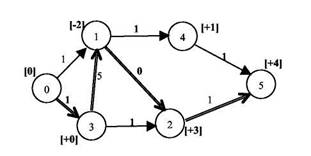
Известны множество методов решения задачи о назначении [7, 12]. Рассмотрим один из них на следующем примере. Пусть имеются n = 3 работника и столько же работ. Матрица
1 2 3 затрат имеет вид: 2 4 7. 5 3 8 Алгоритм 8. Шаг 0. Назначаем каждого человека на самую дешевую для него работу (назначение выделено на рисунке 5 тонкими дугами),
0 Г 1 , если s ij = min s ik то есть положим х и = < * . Если при этом [0, в противном случае назначение является допустимым (то есть все работы выполняют ся), то решение получено. Если имеется «дисбаланс», то есть не
и все работы выполняются (3/?: V * х у > 1), то переходим к сле- дующему шагу.
Шаг k . Введем два подмножества множества дуг: P 1 = {( i ; j ) | Ху = 1}, P2 = {( i ; j ) | Ху = 0}. Примем множество вершин-работ, на которых назначено несколько работников за вход сети, множество вершин-работ, которые не выполняются - за выход сети. Изменим направления дуг из множества P 1 на обратные и примем их длины равными (- s ij ), длины дуг из множества P2 примем равными sij . Найдем путь fjt минимальной длины в полученной сети (потенциалы вершин, вычисляемые при нахождении кратчайшего пути в рассматриваемом примере, приведены в квадратных скобках).
к Ur \ если ( i ; j )*
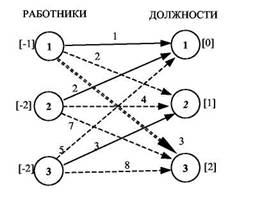
n k 3 [1-хр, если (г; у) е/ В результате в рассматриваемом примере за один шаг получим оптимальное назначение, отличающееся от найденного на нулевом шаге тем, что первому работнику назначается третья работа (см. дугу, обозначенную двойными линиями на рисунке 5). На каждом шаге число «дисбалансов» уменьшается на едини цу. Следовательно, число шагов алгоритма не превышает числа «дисбалансов», которое конечно. Аналогичным способом можно решить любую транспортную задачу (искать кратчайший путь из множества вершин, в которые доставили товара больше, чем требуется, во множество вершин, где товара не хватает). Решение общего случая задачи о потоке минимальной стоимо сти основывается на рассмотрении двойственной задачи [7, 12]. 5. Задачи калспдарпо-сстсвого планирования и управления Рассмотрим проект, состоящий из набора операций (работ). Технологическая зависимость между операциями задается в виде сети {сетевого графика). При этом дуги сети соответствуют опе рациям, а вершины - событиям (моментам окончания одной или нескольких операций). Для каждой операции ( i ; j ) задана ее продолжительность tij . Методы описания и исследования сетевых графиков изучаются в теории календарно-сетевого планирования и управления (КСПУ) [2, 3, 7, 8, 10, 11, 16]. Задача определения продолжительности проекта (управле ние временем). Легко видеть, что продолжительность проекта определяется путем максимальной длины, называемым критическим путем. Методы поиска пути максимальной длины описаны выше. Критический путь в сети на рисунке 6 выделен двойными дугами и равен 16.
Рис. 6. Поиск критического пути Операции, принадлежащие критическому пути, называются критическими. Остальные (некритические) операции имеют резерв времени, характеризуемый максимальной задержкой операции, при которой продолжительность проекта не изменяется. Критические операции имеют нулевой резерв. Приведем соответствующие формулы. Алгоритм 9. Предположим, что выполнение комплекса опера ций (проекта) начинается в нулевой момент времени. Обозначим Q 0 - множество событий, не требующих выполнения ни одной из операций, то есть входы сети с правильной нумерацией; Q i - множество событий, непосредственно предшествующих событию i , то есть множество вершину сети, для которых существует дуга ( j ; i ). Положим (1) Величина tj называется ранним моментом {временем) свер шения г - ro события и характеризует время, раньше которого это событие произойти не может. Длина критического пути (2) определяется ранним временем свершения конечного события, то есть события, заключающегося в завершении всех операций. Поздним моментом венно следующих за событием i , то есть множество вершину сети, для которых существует дуга ( i ; j ). Вычислим для каждой вершины-события i длину l i максимального пути от этой вершины до выхода сети - события, заключающегося в завершении всего ком плекса операций: (3) Положим Для завершения проекта за время T необходимо и достаточно, чтобы
событие i произошло не позднее момента Полным резервом At t события i называется разность между его поздним и ранним моментами свершения, то есть (4) Очевидно, полный резерв критических событий (событий, принад лежащих критическому пути) равен нулю.
Задачи распределения ресурса на сетях удобно рассматри
вать, изображая операции вершинами сети, а зависимости - дугами (представления
«операции-дуги, события-вершины» и «зависимости-дуги, операции-вершины»
эквивалентны [10]). Пунктиром могут быть отражены ресурсные зависимости - когда
для выполнения одних и тех же операций должны быть использованы одни и те
же ресурсы. Примером могут являться сети, изображенные на рисунках 6 и 7.
Полным резервом операции ( i ; j )
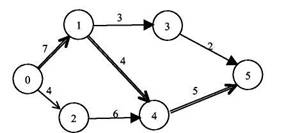
называется вели чина Для определения оптимального распределения ресурса необ ходимо найти критические пути для каждого из вариантов распре деления ресурса и сравнить длины этих путей (в сети, приведенной на рисунке 7, существует общий для операций «0-1» и «0-2» ресурс; потенциалы вершин, соответствующие различным способам использования этого ресурса - сначала выполняется операция «0-1», затем «0-2» и наоборот, приведены на рисунке 7 соответствен но в квадратных скобках и без скобок). Универсальных эффективных точных методов решения задач распределения ресурсов на сетях не существует. В качестве част ного случая, для которого существует простой алгоритм, приведем следующий пример. В сети, изображенной на рисунке 8, для трех операций извест ны поздние времена окончания т ,. Требуется определить очеред ность выполнения этих трех операций при условии, что все опера ции выполняются одной единицей ресурса и поэтому не могут выполняться одновременно.
Рис. 8. Пример распределения ресурса Легко показать, что в рассматриваемом примере оптимально выполнять первой операцию с минимальным т,. Если для выполнения проекта выделено ограниченное количе ство ресурса,
то возникает задача наилучшего его использования. Обозначим w i - объем г-ой
операции, t , то момент ti ее окончания определяется как минимальное время, удовлетворяющее уравнению: (5) Если количество ресурса, используемое при выполнении неко торой операции, не изменяется во времени, то говорят, что она выполняется с постоянной интенсивностью. Тогда продолжительность операции определяется выражением (6) t i ( v i ) = w i / fi ( v i ). В настоящее время общих алгоритмов поиска распределения ограниченных ресурсов между операциями, минимизирующего время завершения проекта, не существует. Поэтому рассмотрим несколько частных случаев. Пусть все операции независимы и выполняются ресурсом одного вида, количество которого равно R , a f i ( v i ) - непрерывные строго монотонные вогнутые функции. Тогда существует оптимальное решение, в котором каждая операция выполняется с по стоянной интенсивностью и все операции заканчиваются одновре менно в момент времени T, определяемый как минимальное время, удовлетворяющее следующему неравенству: (7) где Эвристические алгоритмы определения оптимального распре деления ресурса для ряда случаев «невогнутых» функций интен сивности рассматриваются в [1-4]. Обширный класс задач КСПУ составляют задачи агрегирования - представления комплекса операций (проекта) в виде одной операции и исследования свойств таких представлений, для кото рых оптимизация в рамках агрегированного описания дает реше ние, оптимальное для исходного (детального) описания. Основные подходы к постановке и решению задач агрегирования рассматриваются в [1,2, 10, 16]. Литература • Баркалов С.А., Бурков В.Н., Новиков Д.А., Шульженко Н.А. Модели и
меха • Баркалов С.А., Бурков В.Н., Гилязов Н.М. Методы агрегирования в
управле • Баркалов С.А., Бурков В.Н. Минимизация упущенной выгоды в задачах
• Баркалов С.А., Бурков В.Н., Курочка П.Н., Образцов Н.Н. Задачи
управления • Берж К. Теория графов и ее применения. М.: Иностранная литература,
1962. — • Бурков В.Н., Багатурова О.С., Иванова СИ. Оптимизация обменных
производ • Бурков В.Н., Горгидзе И.А., Ловецкий СЕ. Прикладные задачи теории
графов. • Бурков В.Н., Заложнев А.Ю., Новиков Д.А. Теория графов в управлении
• Бурков В.Н., Зинченко В.Н., Сочнев СВ., Хулап Г.С Механизмы обмена в
• Бурков В.Н., Ланда Б.Д., Ловецкий СБ., Тейман А.И., Чернышев В.Н.
Сетевые • Бурков В.Н., Новиков Д. А. Как управлять проектами. М.: Синтег , 1997. — 188 с. • Вагнер Г. Основы исследования операций. М.: Мир, 1972. Т. 1—4. • Воронин А.А., Мишин СП. Оптимальн ые ие рархические структуры. М.:
ИЛУ • Егоршин А.П. Управление персоналом. Н. Новгород: НИМБ, 1997. — 607 с . • Емеличев В.А ,, Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции
по • Колосова Е.В., Новиков Д.А., Цветков А.В. Методика освоенного объема
в • Коргин Н.А. Механизмы обмена в активных системах. М.: ИЛУ РАН, 2003. • Новиков Д. А. Сетевые структуры и организационные системы. М.: ИЛУ
РАН, • Оре О. Теория графов. М.: Наука, 1968. - 352 с . | ||||||||
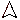

 Выход
Выход