|
Элементы произвольного массива  можно рассматривать как узлы дерева, для которых индексы
массива имеют назначения, аналогичные тем, которые они имели в турнике с
выбыванием: можно рассматривать как узлы дерева, для которых индексы
массива имеют назначения, аналогичные тем, которые они имели в турнике с
выбыванием:
i =1 – корень дерева,
2 i – левый сын i -
го элемента,
2 i +1 – правый сын i
-го элемента,
i /2 – отец i -го элемента.
Информационная часть i -го элемента будет равна
x [ i ] . Здесь
i /2 – целая часть дроби 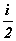 . Если для всех
i , таких, что . Если для всех
i , таких, что 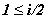 и и 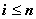 , имеют место
неравенства , имеют место
неравенства 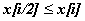 , то массив
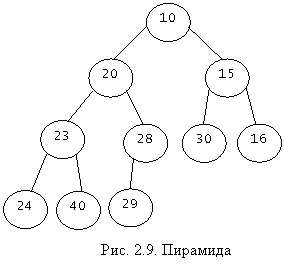
называется пирамидой . На рис изображена
пирамида, состоящая из 10 элементов. , то массив
называется пирамидой . На рис изображена
пирамида, состоящая из 10 элементов.
Она соотвествует массиву
x 1 =10, x 2 =20, x 3 =15, x 4 =23, x 5 =28, x 6 =30, x 7 =16, x 8 =24, x 9
=40, x 10 =29.
 Обобщим понятие пирамидальности на части массива. Массив x
называется пирамидальным в части
l : u , где
1 ? l
? u
? n , если
неравенство x[i/2] ? x[i]
имеет место для каждого i ,
удовлетворяющего соотношениям l ? i/2
и i ? u . Обобщим понятие пирамидальности на части массива. Массив x
называется пирамидальным в части
l : u , где
1 ? l
? u
? n , если
неравенство x[i/2] ? x[i]
имеет место для каждого i ,
удовлетворяющего соотношениям l ? i/2
и i ? u .
 Если к пирамиде добавить элемент x n +1 , то
свойство пирамидальности в части 1: n
за Если к пирамиде добавить элемент x n +1 , то
свойство пирамидальности в части 1: n
за  шагов можно
расширить до свойства пирамидальности в части 1:
n +1 , меняя в цикле местами с отцом
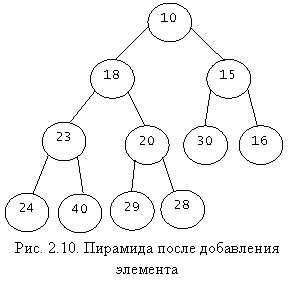
элемент, в котором нарушается свойство пирамидальности. Например
, если к пирамиде на рис добавить x 11 =18
, то надо переставить местами элементы 18 и 28, а потом – 18 и 20.
Получим пирамиду, приведенную на рис. шагов можно
расширить до свойства пирамидальности в части 1:
n +1 , меняя в цикле местами с отцом
элемент, в котором нарушается свойство пирамидальности. Например
, если к пирамиде на рис добавить x 11 =18
, то надо переставить местами элементы 18 и 28, а потом – 18 и 20.
Получим пирамиду, приведенную на рис.
Пусть SiftUp ( int i ) – подпрограмма, расширяющая свойство пирамидальности в
части 1: i -1 до свойства
пирамидальности в части 1: i
. Тогда легко построить пирамиду, состоящую из элементов массива
x [1],..., x [ n
]. Это делается с помощью цикла
for ( i =2; i <= n ; i ++)
SiftUp ( i );
после которого
1271
наименьший элемент массива будет находиться в корне и будет
равен x [1].
Если теперь выбрать этот наименьший элемент и на его место поставить
последний элемент, то для нахождения наименьшего среди оставшихся достаточно
расширить свойство пирамидальности в части 2: n -1 до пирамидальности массива x
в части 1: n -1 . Повторение этого процесса приводит к одному из видов
сортировки выбором – к пирамидальной сортировке .
Пусть SiftDown ( int i ) – подпрограмма, расширяющая свойство пирамидальности
массива x в части 2: i до свойства пирамидальности в части 1: i . Тогда для
реализации пирамидальной сортировки достаточно следующих операторов:
for(i=2; i<=n; i++)
SiftUp(i);
for(i=n; i>=2; i--)
{
swap(&x[1], &x[i]; SiftDown(i-1));
}
В первом цикле будет построена пирамида с наименьшим элементом x [1] . Во
втором цикле элемент x [1] переставляется с последним, в результате чего
наименьший элемент оказывается в конце массива. Затем пирамидальность части 2: n
-1 распространяется на часть 1: n -1 . Затем вновь x [1] переставляется с x [ n
-1] и пирамидальность части 2: n -2 распространяется на часть 1: n -2 , и т.д. В
результате элементы массива x будут расположены в порядке невозрастания x [1] ?
x [2] ? ... ? x [ n ].
Разработаем подпрограммы SiftUp () и SiftDown (). Расширение пирамидальности
в части 1: n -1 до пирамидальности в части 1: n осуществляется сравнением x [ n
] с предками узла n .
void SiftUp(int n)
// Heap(1,n-1) ? Heap(1,n)
{
int i = n , p ;
while ( i >1) // пока не достигли корня
{
p=i/2; // индекс отца
if(x[p]<=x[i]) break; // выход из цикла
swap(&x[p],&x[i]); // если x[p]>x[i]
i = p ; // движемся наверх
}
}
Расширение пирамидальности в части 2:n до пирамидальности в части 1:n
осуществляется с помощью сравнения x[1] с потомками, и перестановками с меньшими
из них.
void SiftDown(int n)
// Heap(2,n) ? Heap(1,n)
{
int i=1,c;
while((c=2*i)<=n)
{
// c – левый сын узла i
if (( c +1)<= n ) // c +1 – правый сын
if ( x [ c +1]< x [ c ])
c = c +1; // наименьший сын
if(x[i]<=x[c]) break; // выход из цикла
swap (& x [ c ],& x [ i ]); // движение вниз
i = c ;
}
}
Приведем окончательный текст программы для сортировки массива по убыванию.
#include<conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int x[11];
void swap(int *a, int *b)
{
int temp=*a;
*a=*b;
*b=temp;
}
void SiftUp(int n)
{
int i = n , p ;
while ( i >1) //пока не достигнут корень
{
p = i /2; //индекс сдвига
if ( x [ p ]<= x [ i ]) break ; //выход из цикла
swap(&x[p],&x[i]); // если x[p] > x[i]
i = p ; //то движение наверх
}
}
void SiftDown(int n)
{
int i=1,c;
while (( c =2* i )<= n ) //с – левый сын узла
{
if (( c +1)<= n ) //с+1 – пра 49f вый сын узла
if ( x [ c +1]< x [ c ])
c = c +1; //наименьший сын
if(x[i]<=x[c]) break; // выход из цикла
swap (& x [ c ],& x [ i ]); //движение вниз
i=c;
}
}
main()
{
int i;
randomize();
for(i=1; i<=10; i++)
x[i]=rand();
clrscr();
printf(" До сортировки :\n");
for(i=1; i<=10; i++)
printf("%d ",x[i]);
for(i=2; i<=10; i++)
SiftUp(i);
for(i=10; i>=2; i--)
{
swap(&x[1], &x[i]);
SiftDown(i-1);
}
printf("\n После сортировки :\n");
for(i=1; i<=10; i++)
printf("%d ",x[i]);
}
Результаты работы программы
До сортировки:
30316 7564 18987 7484 5556 25673 1984 21007 18977 18770
После сортировки:
30316 25673 21007 18987 18977 18770 7564 7484 5556 1984
Новый исходник:
Код на C++ #include<conio.h> #include <iostream.h> #include <stdlib.h> class Racio { public: float chisl;//числитель float znamen;//знаменатель Racio() {};//конструктор по умолчанию Racio(float c, float z) { chisl=c; znamen=z; socr(); }//конструктор ~Racio() {}//деструктор void socr() //сокращение { if(znamen==0) {cout << "Ошибка"; exit(1);}//ноль недопустим float a=chisl; float b=znamen; if(chisl==0) {znamen=1;return;}//ноль недопустим if(a<0){a=-a;}; if(b<0){b=-b;}; //Сокращение дроби while (a!=b) { if(a>b) a=a-b; if(b>a) b=b-a; } chisl=chisl/a; znamen=znamen/a; } int operator==(Racio &obj);//перегрузка оператора = void operator=(Racio &obj);//перегрузка оператора == int operator<(Racio &obj);//перегрузка оператора < int operator<=(Racio &obj);//перегрузка оператора <= int operator>(Racio &obj);//перегрузка оператора > int operator>=(Racio &obj);//перегрузка оператора >= // Перегрузка оператора << для вывода класса Racio friend ostream &operator<<(ostream &, Racio &); }; //Перегрузка == int Racio::operator==(Racio &obj) { if(chisl==obj.chisl&&znamen==obj.znamen)return 1; else return 0; } //Перегрузка = void Racio::operator=(Racio &obj) { chisl=obj.chisl; znamen=obj.znamen; } //Перегрузка < int Racio::operator<(Racio &obj) { float d1=chisl/znamen; float d2=obj.chisl/obj.znamen; if(d1<d2)return 1; return 0; } //Перегрузка <= int Racio::operator<=(Racio &obj) { float d1=chisl/znamen; float d2=obj.chisl/obj.znamen; if(d1<=d2)return 1; return 0; } //Перегрузка > int Racio::operator>(Racio &obj) { float d1=chisl/znamen; float d2=obj.chisl/obj.znamen; if(d1>d2)return 1; return 0; } //Перегрузка >= int Racio::operator>=(Racio &obj) { float d1=chisl/znamen; float d2=obj.chisl/obj.znamen; if(d1>=d2)return 1; return 0; } //Перегрузка оператора << ostream &operator<< (ostream &fo, Racio &fp) { fo << fp.chisl << "/" <<fp.znamen<<" "; return fo; } template <class Type> void swap(Type *a, Type *b) { Type temp=*a; *a=*b; *b=temp; } template <class Type> void SiftUp(Type *x,int n) { int i=n,p; while(i>1) //пока не достигнут корень { p=i/2; //индекс сдвига if(x[p]>=x[i]) break; //выход из цикла swap(&x[p],&x[i]); //если x[p] > x[i] i=p; //то движение наверх } } template <class Type> void SiftDown(Type *x,int n) { int i=1,c; while((c=2*i)<=n) //с – левый сын узла { if((c+1)<=n) //с+1 – правый сын узла if(x[c+1]>x[c]) c=c+1; //наименьший сын if(x[i]>=x[c]) break; //выход из цикла swap(&x[c],&x[i]); //движение вниз i=c; } } main() { clrscr(); gotoxy(25,1); cout<<"ПИРАМИДАЛЬНАЯ СОРТИРОВКА"; int y[11]; int i; randomize(); for(i=1; i<=10; i++) y[i]=random(10); cout<<"\nРяд целых чисел"<<'\n'; for(i=1; i<=10; i++) cout<<' '<<y[i]; for(i=2; i<=10; i++) SiftUp(y,i); for(i=10; i>=2; i--) { swap(&y[1], &y[i]); SiftDown(y,i-1); } cout<<"\nОтсортированный ряд"<<'\n'; for(i=1; i<=10; i++) cout<<' '<<y[i]; float x[11]; for(i=1; i<=10; i++) x[i]=random(10)*0.1; cout<<"\n\nРяд чисел c плавующей точкой"<<'\n'; for(i=1; i<=10; i++) cout<<' '<<x[i]; for(i=2; i<=10; i++) SiftUp(x,i); for(i=10; i>=2; i--) { swap(&x[1], &x[i]); SiftDown(x,i-1); } cout<<"\nОтсортированный ряд"<<'\n'; for(i=1; i<=10; i++) cout<<' '<<x[i]; //Рациональные числа Racio r[11]; float xi; for(i=1; i<=10; i++) { //r[i].chisl=random(8)+1; r[i]=Racio(random(8)-5,random(10)+1); //do{r[i].znamen=random(10)+1;}while(r[i].znamen<=r[i].chisl); //r[i].socr(); } cout<<"\n\nРяд рациональных чисел "<<'\n'; for(i=1; i<=10; i++) cout<<' '<<r[i]; for(i=2; i<=10; i++) SiftUp(r,i); for(i=10; i>=2; i--) { swap(&r[1], &r[i]); SiftDown(r,i-1); } cout<<"\nОтсортированный ряд"<<'\n'; for(i=1; i<=10; i++) cout<<' '<<r[i]; getch(); return 0; }
| 

 Выход
Выход Обобщим понятие пирамидальности на части массива. Массив x
называется пирамидальным в части
l : u , где
1 ? l
? u
? n , если
неравенство x[i/2] ? x[i]
имеет место для каждого i ,
удовлетворяющего соотношениям l ? i/2
и i ? u .
Обобщим понятие пирамидальности на части массива. Массив x
называется пирамидальным в части
l : u , где
1 ? l
? u
? n , если
неравенство x[i/2] ? x[i]
имеет место для каждого i ,
удовлетворяющего соотношениям l ? i/2
и i ? u .  Если к пирамиде добавить элемент x n +1 , то
свойство пирамидальности в части 1: n
за
Если к пирамиде добавить элемент x n +1 , то
свойство пирамидальности в части 1: n
за