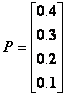Вопрос 8. Нечеткая и вероятностная логики: основные свойства, достоинства и недостатки. Привести пример, демонстрирующий основное отличие нечеткой и вероятностной логик.
| Добавил: | DMT | ||||||||||||||||||||||||
| Дата создания: | 30 декабря 2007, 19:07 | ||||||||||||||||||||||||
| Дата обновления: | 22 января 2008, 21:17 | ||||||||||||||||||||||||
| Просмотров: | 11200 последний сегодня, 3:44 | ||||||||||||||||||||||||
| Комментариев: | 0 | ||||||||||||||||||||||||
|
Вопрос 8. Нечеткая и вероятностная логики: основные свойства, достоинства
и недостатки. Привести пример, демонстрирующий основное отличие нечеткой и
вероятностной логик.
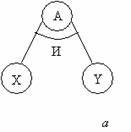
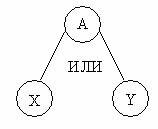
Нечеткая логика Нечеткая логика, выделившаяся из теории нечетких множеств, — это разновидность непрерывной логики, в которой логические формулы могут принимать истинностные значения между 1 и 0. В нечеткой логике достоверность представляется как истинностное значение между 1 и 0, и значения, приписанные правилам на рис. 6.8, это и есть истинностные значения (вероятность определяется в статистическом смысле, и в отличие от нее истинностное значение это некоторое произвольное субъективное значение, не имеющее никакого статистического смысла). Пусть t x и t y —истинностные значения предпосылок Х и Y некоторого правила, тогда истинностное значение t предпосылки в случае связей И и ИЛИ на рис. 40, а, б определяется следующим образом.
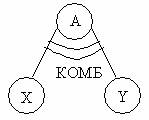
1. При связи И t предпосылки = min { t x , t y }. (6.18) 2. При связи ИЛИ t предпосылки = max { t x , t y }. (6.19) Если в общем случае t правила есть истинностное значение, приписанное правилу, то истинностное значение t A , распределенное на вывод, определяется как t A = min { t предпосылки , t правила ). (6.20) Определение минимума — это идея, свойственная нечеткой логике и отличающая ее от других методов (в которых производится умножение). Связь КОМБ на рис. 40. особо не оговаривается. В качестве такой связи можно рассматривать одну из связей И или ИЛИ. Собственно говоря, в нечеткой логике и нечетких выводах рассматривается случай, когда множества X, Y , А и другие, описанные в предпосылках и выводах правил, суть нечеткие множества.
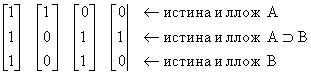
Вероятностная логика Нильсон предложил идею расширения логики и ввел понятие вероятностной логики, в которой всем логическим формулам приписывается вероятность. Здесь вероятность вновь соответствует законам Байеса. Связь логики и вероятности важна также с точки зрения рационального построения новой теории на основе теории логического моделирования. И хотя эта' теория еще не доведена до использования на уровне вычислений, ознакомимся с ней на простых примерах. Рассмотрим три логических формулы в логике высказываний: А , А E В , В. Представим следующие вертикальные векторы
1 2 3 4
где 1 — мир истинности А, А E В, В, 2 — мир истинности А и лжи А E В, В, 3 — мир лжи А и истинности А E В, В, 4 — мир лжи А, В и истинности А E В. А именно, 1 и 0 обозначают истину и ложь высказывания А в первой строке вертикальной векторов, А E В во второй строке и В в третьей строке. Эти три логические формулы подобраны так, что возможны только четыре указанных выше случая (когда нет противоречия). Это так называемые возможные миры (миры с возможностью интерпретации). Все другие миры— например А, А E В истина, В ложь — это миры, содержащие противоречие. Если выбрать один из возможных миров, то образуется традиционная двузначная логика. В вероятностной логике рассматриваются состояния, когда одновременно с некоторой вероятностью могут существовать несколько возможных миров. Например, пусть вероятность, с которой возможна интерпретация в мире 1, равна 0,4, а вероятности интерпретации в мирах 2,3,4 соответственно равны 0,3, 0,2, 0,1 (сумма вероятностей возможных миров равна 1), тогда представим следующим образом вектор вероятностей возможных миров
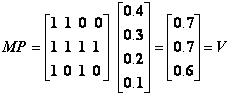
И наоборот, если существует группа логических формул, каждой из которых приписана некоторая вероятность, то эту группу можно считать упорядоченной (непротиворечивой), только когда возможно вероятностное существование соответствующих возможных миров. Если построить матрицу М , элементами которой служат вертикальные векторы, представляющие возможные миры, то с помощью матричной операции МР = V можно вычислить вероятности выбора каждой логической формулы. В данном примере
А именно, эти вероятностные возможные миры имеют состояние «истина» с вероятностью 0,7 ( А ), 0,7 ,( А E В ) и 0,6 ( В ). Пусть задана вероятность А р ( А ) и вероятность А E В р ( А E В ), тогда вероятность В р ( В ) должна находиться в диапазоне
Таким образом, можно определить логический вывод (с вероятностью). Различие нечеткой и вероятностной логики.
Пример: действие сложить 1 + 1. В вероятностной логике есть вероятность, что сложение будет означать арифметическую операцию, а не иметь другой смысл (родитель + родитель равно ребенок). Вероятность арифметической операции с исходом 2 равна 0,99, а отображения связи родитель+родитель=ребенок равна 0,01, но это статистическая величина, не зависящая от какого-либо субъективного мнения. При сложении 1+1 в нечеткой логике значениям 1 и 1 будет присвоены субъективные истинностные значения. Формула всегда работает однозначно, но результат тоже имеет истинностное значение на интервале [0 1].
| |||||||||||||||||||||||||

 Выход
Выход