Вопрос 7. Инженерия знаний и нечеткость. Классификация видов нечеткости. Привести пример формулировки задач для основных видов нечеткости.
| Добавил: | DMT |
| Дата создания: | 30 декабря 2007, 19:06 |
| Дата обновления: | 22 января 2008, 21:16 |
| Просмотров: | 15951 последний 23 апреля, 0:54 |
| Комментариев: | 0 |
|
Вопрос 7. Инженерия знаний и нечеткость. Классификация видов нечеткости.
Привести пример формулировки задач для основных видов нечеткости.
Инженерия знаний (knowledge engineering) – одно из важных направлений современного программирования, занимающееся развитием языков, методов и систем представления и обработки знаний на компьютерах. Оно возникло в 1950-х гг. как один из разделов искусственного интеллекта, так как стало необходимо явным образом (отдельно от программ) хранить, изменять и пополнять базы знаний, содержащие в обобщенном виде необходимую для решения задач информацию о предметной области. Как выяснилось, знания, необходимые для решения многих нетривиальных практических задач с использованием компьютеров, носят гибридный характер , то есть, требуются не только процедурные знания (алгоритмы, их программные реализации и типовые процедуры решения задач), но также концептуальные знания (определения концепций проблемной области и отношений между ними), фактуальные знания (конкретные факты и их связи между собой) и эвристические знания (неформальные правила рассуждений, отражающие практический опыт решения задач в проблемной области). Правила (конструкции вида ЕСЛИ условие ТО действие, используемые для продукционного вывода, при котором на каждом шаге, при истинности условия некоторого выбранного правила, активизируется его действие) удобны для представления эвристических знаний и структурируются в виде наборов правил (rule sets), каждый из которых применяется для вывода некоторого целевого утверждения (goal); - фреймы (frames) – иерархические структуры, удобные для представления знаний о концепциях и их взаимосвязи ; фреймы могут использоваться не только для представления структур знаний, но и для сопоставления с объектами исследуемой проблемной области, с целью их анализа и классификации; - семантические сети (semantic nets) – нагруженные ориентированные мультиграфы, которые, как и фреймы, удобны для представления концепций и их взаимоотношений и являются, по-видимому, наиболее общей формой представления знаний. Плохо поставленные (некорректные) задачи существуют во всех предметных областях, где, как ожидается, будут эффективными интеллектуальные системы как средство построения информационных систем нового поколения. К ним относятся проблемы, строгое описание которых невозможно, а также сложные проблемы. Корректные задачи часто можно решить существующими методами систематизации и программирования. В области некорректных задач точные знания нельзя получить, либо их нельзя получить сразу, поэтому, как правило, необходим подход, суть которого в постепенном приближении к полному набору знаний. Другими словами, знания чаще всего нечетки. Для того чтобы интеллектуальные системы вышли за рамки простых символьных выводов и приблизились к мышлению человека, необходимы методы представления нечетких знаний и механизм выводов, работающий в их среде. Человек обладает самыми различными формами знаний, и пока еще не совсем ясно, каким образом они структурированы в его мозгу. Однако для использования знаний в компьютерах они должны быть формализованы и описаны. В этом состоит проблема представления знаний. Пока знания не формализованы и не описаны, они не могут быть использованы в компьютерах, точно так же не могут быть использованы техническими средствами и нечеткости, предварительно не описанные в некоторой форме. Все нечеткости, с которыми до сих пор приходилось иметь дело в инженерии знаний, можно классифицировать следующим образом: 1) недетерминированность выводов, 2) многозначность, 3) ненадежность, 4) неполнота, 5) нечеткость или неточность. Недетерминированность выводов (Нечеткий вывод???) Недетерминированное управление выводами наиболее характерно для систем искусственного интеллекта. Такое управление необходимо потому, что знания накапливаются фрагментарно, и нельзя априори определить цепочку логических выводов, в которых они используются. Другими словами, необходимо методом проб и ошибок выбрать некую цепочку выводов, и в случае неуспеха организовать перебор с возвратами для поиска другой цепочки и т. д. Такое управление является предпосылкой проявления гибкости и интеллектуальных способностей, позволяющих найти выход в самых различных ситуациях. Поскольку эффективность простого поиска низка, возникает необходимость определения пути, по которому следует начать поиск в первую очередь. При эвристическом поиске, разработанном на первых этапах исследования искусственного интеллекта, руководствуются оценочными функциями, которые не всегда бывают точными (имеют априорные значения). Большинство поисковых задач можно сформулировать как задачи поиска в пространстве состояний пути от исходного состояния заданной задачи до целевого состояния путем повторения возможных преобразований (с помощью операторов). При этом для организации поиска в пространстве состояний удобно использовать дерево поиска (или его более общую форму — граф). К основным методам систематического просмотра пространства состояний относятся вертикальный и горизонтальный поиск. В эпоху инженерии знаний возникла идея реализации выводов (поиска) на основе знаний. Шире стали применять эвристические знания (в смысле не обязательно достоверных знаний, т. е. знаний, содержащих нечеткости). Нечеткий вывод: дедукция (от частного к общему), индукция (от общего к частному). Пусть есть нечеткий множества F , G , F `, G `. Если F = G , тогда вывод F ` из G ` производится по F = G . В случае нечеткого множества F и F ` могут не совпадать. Нечеткий вывод можно произвести, если F близко к F ` и их можно сопоставить. Пример: если Петя – маленький, то Вася – взрослый. Пете около 5. Сколько тогда Васе? Многозначность. Многозначность интерпретации — обычное явление при понимании естественных языков и распознавании изображений и речи. При понимании естественных языков большими проблемами становятся многозначность смысла слов, многозначность их подчиненности, многозначность местоимений в контексте и т. п. Как правило, устранение многозначности обеспечивается за счет более широкого контекста и семантических ограничений. При обработке изображений часто многозначна интерпретация элементов изображения (контуры, области и т. п.). В общем случае устранить многозначность помогают более широкие пространственные отношения и другие способы. Метод релаксации— это метод систематического устранения многозначности при интерпретации изображений с помощью циклических операций. Пример: казнить нельзя помиловать. Где поставить запятую? Нарисованы несколько соединенных кубов. Какие грани выпуклые, а какие впуклые? Салат рекурсивный: помидоры, огурцы, салат. Ненадежность В задачах, которые решают интеллектуальные системы, иногда приходится применять ненадежные знания и факты, представить которые двумя значениями — истина или ложь (1 или 0)—трудно. Существуют знания, достоверность которых, скажем, 0,7. Такую ненадежность в современной физике и технике представляют вероятностью, подчиняющейся законам Байеса (для удобства назовем ее байесовской вероятностью), но в инженерии знаний было бы нелогично иметь дело со степенью надежности, приписанной знаниям изначально, как с байесовской вероятностью, (нелогично незнание представлять байесовской вероятностью). Поэтому одним из первых был разработан метод использования коэффициентов уверенности. Этот метод не имеет теоретического подкрепления, но стал примером обработки ненадежных знаний. Позже была введена теория вероятностей Демпстера — Шафера, которая имеет все признаки математической теории. По сравнению с байесовской вероятностью теория Демпстера — Шафера отличается тем, что она не фиксирует значения вероятности, а может представлять и незнание. Связь между подзадачами, на которые разбита задача, оперирующая двумя понятиями — истина и ложь, может быть представлена через операции И и ИЛИ . В задачах с ненадежными исходными данными кроме И и ИЛИ важную роль играет комбинированная связь, которую будем обозначать как КОМБ . Такая связь независимо подкрепляет или опровергает цель на основании двух и более доказательств. Для решения сложных задач можно использовать метод разбиения их на несколько подзадач. Каждая подзадача в свою очередь разбивается на простые подзадачи, поэтому задача в целом описывается иерархически. Знания, которые по условиям подзадач определяют условия задач высшего уровня, накапливаются фрагментарно. В задачах с ненадежными данными знания могут не только иметь степень надежности, равную 1, но и промежуточные значения между истиной и ложью. На основании двух и более доказательств цели (или подцели) независимо подтверждаются или опровергаются (в случае противоречивых доказательств), если связь комбинированная. Например, рассмотрим случай определения (диагностирования), простужен ли больной. Пусть доказательство 1 — кашель у больного — надежно со степенью 0,6, а доказательство 2 — температура 39—40°—надежно со степенью только 0,5. Простудное состояние при наблюдении только одного из доказательств простуды можно подтвердить только с надежностью 0,6 или 0,5. На основании двух и более доказательств цели (или подцели) независимо подтверждаются или опровергаются (в случае противоречивых доказательств), если связь комбинированная. Например, рассмотрим случай определения (диагностирования), простужен ли больной. Пусть доказательство 1 — кашель у больного — надежно со степенью 0,6, а доказательство 2 — температура 39—40°—надежно со степенью только 0,5. Простудное состояние при наблюдении только одного из доказательств простуды можно подтвердить только с надежностью 0,6 или 0,5.
Неполнота Полностью описать мир задач чрезвычайно сложно. Например, знание «птицы летают» — верное, однако встречаются и нелетающие птицы, т. е. это неполное значение. Другой пример: можно перечислить все предметы, которые находятся в комнате, но того, чего в ней нет, перечислить невозможно, поскольку это бесчисленное множество предметов. Точно так же можно перечислить верные знания (в некоторой проблемной области), но перечислить неверные знания и разумно их определить невозможно. Поэтому удобно в базе знаний определять исключительно верные знания, а все, что не определено, считать заведомо неверным. Утверждения, которые не упомянуты ни как истинные, ни как ложные, принято относить к ложным. Это называют гипотезой закрытого мира. Классическая логика исходит из предпосылки, что набор определенных в ней аксиом (знаний) полон, и правильный вывод не меняется, даже если впоследствии добавлена новая аксиома. Такое свойство называется монотонностью. Если допустить, что в базу знаний добавлено такое знание: «как правило, птицы летают (за некоторым исключением)», то обнаружится свойство немонотонных выводов. А именно, при добавлении новой аксиомы иногда возможно отрицание вывода, который считался верным в некоторой системе аксиом (базе знаний). К системам, связанным с неполными знаниями и управлением такими знаниями, относится система поддержания значений истинности. В базе знаний этой системы, неполной и содержащей противоречия, все знания делятся на достоверные и недостоверные, и предусмотрено упорядочение базы с целью устранения недостоверных знаний. В этой системе достоверно истинные знания относятся к классу « IN », а знания, истинность которых недостоверна либо в истинность которых нет повода верить, — к классу « OUT ». Если при добавлении новых знаний возникает противоречие, то выполняется повторная проверка классов знаний. Пример: Какова температура кипящей воды? Если мы не можем пополнить знания об атмосферном давлении, то точно на этот вопрос мы ответить не сможем. Нечеткость и неточность. Когда мы говорим «старик», то не ясно, что мы имеем в виду: больше 50? больше 60? больше 70? Одним из методов изучения множеств без уточнения их границ является теория нечетких множеств, которая была предложена Заде в 1965 г . и продолжает развиваться. В теории нечетких множеств большинство ситуаций оценивается приблизительно, а не точно. Необходимость такого подхода вызвана тем, что по мере роста сложности систем, наша неспособность делать точные и, в то же время, значащие утверждения относительно ее поведения. Было предложение ввести специальные обозначения (метки), определяющие более – менее нечеткие понятия и использующие эти метки в последующих рассуждениях. См. нечеткую логику. | |

 Выход
Выход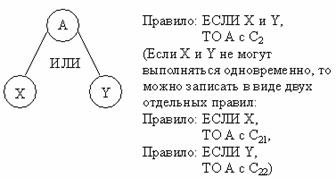
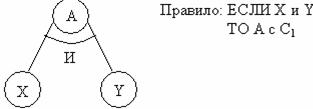
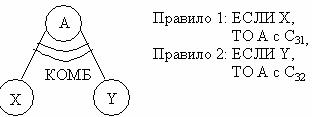 , С ij – степени надежности
, С ij – степени надежности