Вопрос 3. Разработать многопоточную программу для нахождения минимального элемента массива целых чисел методом сдваивания.


Добавил:DMT
Дата создания:30 декабря 2007, 18:20
Дата обновления:30 декабря 2007, 18:20
Просмотров:8013 последний сегодня, 7:46
Комментариев: 2

Вопрос 3. Разработать многопоточную программу для нахождения минимального элемента массива целых чисел методом сдваивания.

up

Комментарии для "Вопрос 3. Разработать многопоточную программу для нахождения минимального элемента массива целых чисел методом сдваивания."


Пользователь: ruslan
Сообщений: 23
Статус: Незримый
Зарегистрирован:
5 января 2008, 2:42
Был:29 января 2008, 21:23
ruslan
smsup 		Дата: 13 января 2008, 1:02 Сообщение № 1
Код на C++
  1. #include <windows.h>  
  2. #include <stdlib.h>  
  3. #include <iostream.h>  
  4. #include <conio.h>  
  5.   
  6. #define N 32		//количество элементов    
  7.   
  8. struct arg		//структура аргументов    
  9. {    
  10.   int l,r,rez;    
  11. };    
  12.     
  13. int x[N]; 		//массив    
  14. //-------------------------  
  15. DWORD WINAPI min(void* s)    
  16. {    
  17.   int i, l=((arg *)s)->l, r=((arg *)s)->r; //заполним переменные    
  18.   if (l==r)    
  19.   {    
  20.     ((arg *)s)->rez = x[l];     //результат    
  21.   }    
  22.   else    
  23.   {//в противном случае вызываем два потока с разными аргументами   
  24.     arg *r1 = new arg, *r2 = new arg;    
  25.     HANDLE H[2];    
  26.     r1->l=l; r1->r=(l+r+1)/2-1;    
  27.     r2->l=(l+r+1)/2; r2->r = r;//после этого создаём потоки    
  28.     H[0]= CreateThread(0,0,min, (void *)r1,0,0);    
  29.     H[1]= CreateThread(0,0,min, (void *)r2,0,0);    
  30.     WaitForMultipleObjects(2,H,true,INFINITE);    
  31.     if(r1->rez < r2->rez)    
  32.       ((arg *)s)->rez = r1->rez;    
  33.     else    
  34.       ((arg *)s)->rez = r2->rez;    
  35.     delete r1; delete r2;    
  36.   }    
  37.   return 1;   //всё прошло успешно    
  38. }    
  39. //---------------------  
  40. int min0()    
  41. {    
  42.   int min=x[0], i;    
  43.   for (i=0; i<N; i++)    
  44.   {    
  45.     if(x[i] < min)    
  46.       min = x[i];    
  47.   }    
  48.   return min;    
  49. }    
  50. //--------------------  
  51. void main()    
  52. {    
  53.   int i;    
  54.   randomize();                          //инициализируем генератор случайных чисел    
  55.   for (i=0; i<N; i++){    
  56.     x[i]=random(100);    
  57.     printf("%d ",x[i]);    
  58.   }    
  59.   arg t;    
  60.   t.l = 0; t.r = N-1;    
  61.   min(&t);                              //находим минальный элемент в потоках    
  62.   cout << "\n min: "<< t.rez;    
  63.   cout << "\n check min: "<< min0();      //проверка    
  64.   getch();    
  65. }    
  66. //---------
При использовании обязательна ссылка на http://DMTSoft.ru
Пользователь: ruslan
Сообщений: 23
Статус: Незримый
Зарегистрирован:
5 января 2008, 2:42
Был:29 января 2008, 21:23
ruslan
smsup 		Дата: 16 января 2008, 0:39 Сообщение № 2
Теория по методу сдваивания

Метод сдваивания.Программу, вычисляющую результат многократного применения ассоциативной бинарной операции, можно реализовать рекурсивно, с помощью функции, аргументом которой являются начальный и конечный индексы массива. Эта функция разбивает массив на две части и затем вызывает себя для обработки каждой из этих частей.

Если каждую функцию преобразовать в функцию потока, загружающую два по-тока, то такой подход приводит к алгоритму параллельного вычисления операции над элементами массива, который называется методом сдваивания.

Пример. Рассмотрим операцию сложения элементов массива, состоящего из n = 2^k. Можно запустить n/2 потоков, вычисляющих суммы x[0]+x[1], x[2]+x[3], …, x[n-2]+x[n-1]. Затем запускаются n/4 потоков, складывающих попарно полученные суммы и т.д. . При n = 8 информационный граф такого алгоритма вычисления суммы изображен на рис. 5.4.

Для вычисления суммы с помощью данного алгоритма рассмотрим рекурсивную функцию, разбивающую массив на два подмассива и вызывающую себя рекурсивно для каждого из этих подмассивов.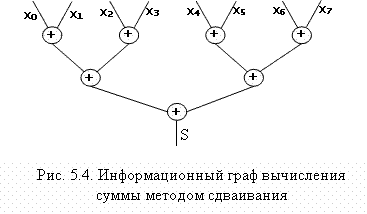


image1


Эта функция будет вызываться в главной программе с помощью оператора S=sum(0, n-1).

Приведём текст рекурсивной функции: 
Код на C++
  1.   
  2. Int Sum(int l, int r) // x[l] + … + x[r]  
  3. {  
  4.   if(l == r) return x[l];  
  5.   else return sum(l, (l + r + 1)/2 - 1) + sum((l + r + 1)/2, r);  
  6. }  
  7.  
При использовании обязательна ссылка на http://DMTSoft.ru