Вопрос 8. Этапы проектирования реляционной БД декомпозиционным методом. Удаление избыточных функциональных зависимостей. Пример: Из данного набора функциональных зависимостей с помощью аксиом вывода удалить все избыточные.
| Добавил: | DMT |
| Дата создания: | 30 декабря 2007, 18:03 |
| Дата обновления: | 30 декабря 2007, 20:32 |
| Просмотров: | 7820 последний сегодня, 0:17 |
| Комментариев: | 0 |
|
Вопрос 8. Этапы проектирования реляционной БД декомпозиционным методом. Удаление избыточных функциональных зависимостей. Пример: Из данного набора функциональных зависимостей с помощью аксиом вывода удалить все избыточные.
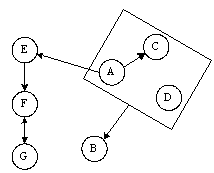
Этапы проектирования: 1) Разрабатывается универсальное отношение для БД (в универсальное отношение включаются все атрибуты, представляющие интерес для данного проектирования; как полагают большинство специалистов, их число не должно превышать двадцати, иначе декомпозиционный метод становится излишне громоздким). 2) Определяются все функциональные зависимости между атрибутами данного отношения. 3) Определяется, находится ли отношение в нормальной форме Бойса - Кодда. Если да, то проектирование завершается, если нет, то осуществляется декомпозиция, т.е. разбиение отношения. 4) Шаги 2) и 3) повторяются для каждого нового отношения, полученного в результате декомпозиции. Проектирование завершается, когда все отношения будут находиться в НФБК. Избыточной функциональной зависимостью называют зависимость, заключающую в себе такую информацию, которая может быть получена на основе других зависимостей из числа использованных при проектировании БД. Пусть r – отношение со схемой R, w , x , y , z – подмножества R. 1-я аксиома вывода. Рефлексивность . В r всегда имеет место Х -> Х (так как отношение 2-я аксиома вывода. Пополнение . Если r удовлетворяет Х -> Y, то r удовлетворяет F-зависимости XZ -> Y (Х -> Y влечет за собой XZ -> Y). 3-я аксиома вывода. Аддитивность (так же известна под названием – объединение). Если отношение r удовлетворяет X -> Y и X -> Z, то r удовлетворяет F-зависимости Х -> YZ. 4-я аксиома вывода. Проективность . Если отношение r удовлетворяет X -> YZ, то r удовлетворяет X -> Y и X -> Z. 5-я аксиома вывода. Транзитивность . Х -> Y и Y -> Z влечет за собой X -> Z. 6-я аксиома вывода. Псевдотранзитивность . Если r удовлетворяет зависимостям X -> Y и YZ -> W, то r удовлетворяет XZ -> W. Исходная диаграмма функциональных зависимостей:
B -> F; B -> G, C ,D -> B, E -> F, F -> G, G -> F, A ,D -> F; A,D -> B Удал им из исходного набора функциональных зависимостей все избыточные: • т.к. A -> F , то A , D -> F – исключим по аксиоме пополнения • т.к. A -> E , E -> F , то A -> F исключим по аксиоме транзитивности • т.к. B -> F , F -> G , то B -> G исключим по аксиоме транзитивности • т.к. A , D -> B ; C , D -> B , то по аксиоме пополнения A , C , D -> B • по аксиоме пополнения если A -> E , то A , D -> E если A , D -> E ; E -> F и A , D -> B ; B -> F , то F транзитивно зависит от A , D и B -> F – избыточная функциональная зависимость
Окончательная диаграмма функциональных зависимостей:
A -> E ; A -> C ; A, C , D -> B, E -> F, F -> G, G -> F, Выполним преобразование исходного отношения r ( A , B , C , D , E , F , G ) в набор НФБК – отношений r 1( F , G ) – НФБК (2 ключа ( F и G ) и 2 детерминанта) r 2( A , B , C , D , E , F ) r 3( E , F ) – НФБК (1 ключ ( E ) и 1 детерминант) r4( A, C, D , B, E) r5( A ,E) r6( A,C,D ,B)– НФБК (1 ключ (A,C,D) и 1 детерминант )
Выполним проверку полученного набора отношений на наличие дублирующихся функциональных зависимостей: F-зависимости в отношении r1: F -> G G -> F F-зависимости в отношении r3: E -> F F-зависимости в отношении r4: A ,C,D -> B A ,C,D -> E A ,C,D -> C Таким образом, в полученном наборе отношений нет F-зависимости, которая появлялась бы более чем в одном отношении.
| |

 Выход
Выход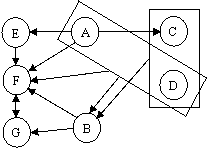
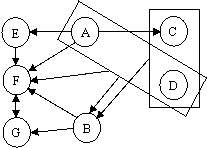 A -> E ; A -> C ; A -> F ,
A -> E ; A -> C ; A -> F ,